【原创】（本小题满分12分）已知一扇形的圆心角为，所在圆的半-优题课

题文

【原创】（本小题满分12分）已知一扇形的圆心角为，所在圆的半径为．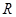
（1）若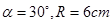，求扇形的弧长及该弧所在的弓形的面积；
（2）若扇形的周长是一定值C （C>0），当α为多少弧度时，该扇形有最大面积？

科目数学题型解答题难度较易

知识点：任意角和弧度制

相关试题

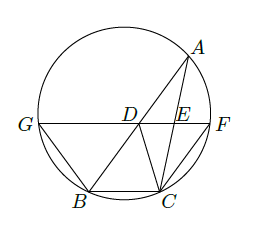
如图， $D, E$ 分别为 $△ A B C$ 边 $A B, A C$ 的中点，直线 $D E$ 交 $△ A B C$ 的外接圆于 $F, G$ 两点，若 $C F ∥ A B$ ，证明：
（1） $C D = B C$ ；
（2） $△ B C D = △ G C B$

已知函数 $f (x)$ 满足满足 $f (x) = f ` (1) e^{x - 1} - f (0) x + \frac{1}{2} x^{2}$ ；
（1）求 $f (x)$ 的解析式及单调区间；
（2）若 $f (x) \geq \frac{1}{2} x^{2} + a x + b$ ，求 $(a + 1) b$ 的最大值.

设抛物线 $C : x^{2} = 2 p y (p > 0)$ 的焦点为 $F$ ,准线为 $l$ , $A \in C$ ,已知以 $F$ 为圆心, $F A$ 为半径的圆 $F$ 交 $l$ 于 $B, D$ 两点；
（1）若 $∠ B F D = 90^{°}$ , $∆ A B D$ 的面积为 $4 \sqrt{2}$ ；求 $p$ 的值及圆 $F$ 的方程；
（2）若 $A, B, F$ 三点在同一直线 $m$ 上，直线 $n$ 与 $m$ 平行，且 $n$ 与 $C$ 只有一个公共点,求坐标原点到 $m, n$ 距离的比值.

如图，直三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中， $A C = B C = \frac{1}{2} A A_{1}$ ， $D$ 是棱 $A A_{1}$ 的中点， $D C_{1} ⊥ B D$ .

（1）证明： $D C_{1} ⊥ B C$

（2）求二面角 $A_{1} - B D - C_{1}$ 的大小.

某花店每天以每枝 $5$ 元的价格从农场购进若干枝玫瑰花，然后以每枝 $10$ 元的价格出售，如果当天卖不完，剩下的玫瑰花作垃圾处理.
（1）若花店一天购进 $16$ 枝玫瑰花，求当天的利润 $y$ (单位：元)关于当天需求量 $n$ （单位：枝， $n \in N$ ）的函数解析式.
（2）花店记录了100天玫瑰花的日需求量（单位：枝），整理得下表：

以100天记录的各需求量的频率作为各需求量发生的概率.
（i）若花店一天购进 $16$ 枝玫瑰花， $X$ 表示当天的利润（单位：元），求 $X$ 的分布列，数学期望及方差；
（ii）若花店计划一天购进16枝或17枝玫瑰花，你认为应购进16枝还是17枝？请说明理由.

试卷网试题网古诗词网作文网范文网