水产养殖专业户王大爷承包了30亩水塘,分别养殖甲鱼和桂鱼.有关成本、销售额见右表:
(1)2012年,王大爷养殖甲鱼20亩,桂鱼10亩.求王大爷这一年共收益多少万元?(收益=销售额-成本)
(2)2013年,王大爷继续用这30亩水塘全部养殖甲鱼和桂鱼,计划投入成本不超过70万元.若每亩养殖的成本、销售额与2012年相同,要获得最大收益,他应养殖甲鱼和桂鱼各多少亩?
(3)已知甲鱼每亩需要饲料500kg,桂鱼每亩需要饲料700kg.根据(2)中的养殖亩数,为了节约运输成本,实际使用的运输车辆每次装载饲料的总量是原计划每次装载总量的2倍,结果运输养殖所需全部饲料比原计划减少了2次.求王大爷原定的运输车辆每次可装载饲料多少kg?
先化简, 再求值: ,其中 是方程 的根
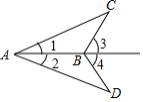
如图,已知 , ,求证: .
已知抛物线的顶点为 并经过点 ,点 在抛物线的对称轴上并且纵坐标为 ,抛物线交 轴于点 .如图1.
(1)求抛物线的解析式;
(2)点 为抛物线对称轴上的一点, 为等腰三角形,求点 的坐标;
(3)如图2,点 为直线 上的一个动点,过点 的直线 与 垂直
①求证:直线 与抛物线总有两个交点;
②设直线 与抛物线交于点 、 (点 在左侧),分别过点 、 作直线 的垂线,垂足分别为 、 .求 的长.

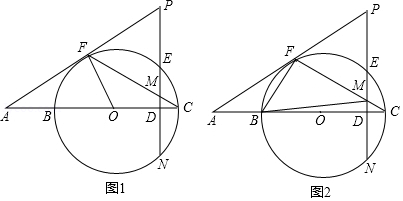
如图1, 是 的直径 上的一点,过 作 交 于 、 , 是 上的一点,过 的直线分别与 、 的延长线相交于 、 ,连接 交 于 , .
(1)求证: 是 的切线;
(2)若 , 的半径为4, ,求 的长;
(3)如图2,在(2)的条件下,连接 、 ;在线段 上有一点 ,并且以 、 、 为顶点的三角形与 相似,求 的长度.
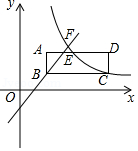
如图,矩形 在平面直角坐标系的第一象限内, 与 轴平行, ,点 的坐标为 , 是 的中点;反比例函数 图象经过点 和点 ,过点 的直线 与反比例函数图象交于点 ,点 的纵坐标为4.
(1)求反比例函数的解析式和点 的坐标;
(2)求直线 的解析式;
(3)直接写出 时,自变量 的取值范围.