已知函数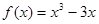
(1)求函数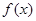 在
在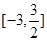 上的最大值和最小值.
上的最大值和最小值.
(2)过点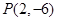 作曲线
作曲线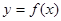 的切线,求此切线的方程.
的切线,求此切线的方程.
在△ABC中,已知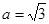 ,
,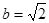 ,B=45°求A、C及c
,B=45°求A、C及c
如图,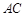 是圆
是圆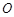 的直径,点
的直径,点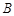 在圆
在圆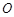 上,
上,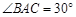 ,
, 交
交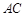 于点
于点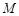 ,
,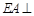 平面
平面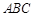 ,
,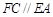 ,
, .
.
(Ⅰ)证明: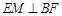 ;
;
(Ⅱ)求平面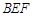 与平面
与平面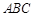 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
在今年伦敦奥运会期间,来自美国和英国的共计6名志愿者被随机地平均分配到跳水、篮球、体操这三个岗位服务,且跳水岗位至少有一名美国志愿者的概率是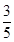 .
.
(Ⅰ)求6名志愿者中来自美国、英国的各几人;
(Ⅱ)求篮球岗位恰好美国人、英国人各一人的概率.
(Ⅲ)设随机变量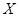 为在体操岗位服务的美国志愿者的个数,求
为在体操岗位服务的美国志愿者的个数,求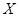 的分布列及期望
的分布列及期望
已知函数 .
.
(Ⅰ)求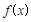 的最小正周期;
的最小正周期;
(Ⅱ)若将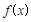 的图象向右平移
的图象向右平移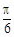 个单位,得到函数
个单位,得到函数 的图象,求函数
的图象,求函数 在区间
在区间 上的最大值和最小值.
上的最大值和最小值.
已知函数 .
.
(Ⅰ)当 时,如果函数
时,如果函数 仅有一个零点,求实数
仅有一个零点,求实数 的取值范围;
的取值范围;
(Ⅱ)当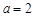 时,试比较
时,试比较 与1的大小;
与1的大小;
(Ⅲ)求证:
 .
.