如图,在三棱锥
中,平面
平面
,
,
. 过点
作
,垂足为
,点
,
分别为棱
,
的中点.
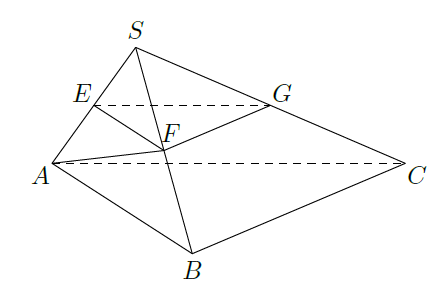
求证:(1)平面
平面
;
(2)
.
(本小题满分14分)
(本题14分).如图所示,在正三棱柱ABC-A1B1C1中,
底面边长和侧棱长都是2,D是侧棱CC1上任意一点,E是
A1B1的中点.
(1)求证:A1B1//平面ABD.
(2)求证:
(3)求三棱锥C-ABE的体积.
(本小题满分12分)已知向量 ,
,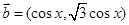 ,函数
,函数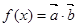 .
.
(1)求函数 的最小正周期和值域;
的最小正周期和值域;
(2)在
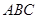 中,
中,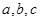 分别是角
分别是角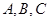 的对边,且
的对边,且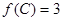 ,
,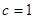 ,
,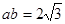 ,且
,且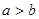 ,求
,求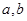
在△ABC中,角A、B、C所对的边分别是a、b、c,则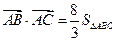 (其中S△ABC为△ABC的面积).
(其中S△ABC为△ABC的面积).
(1)求sin2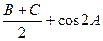 ;
;
(2)若b=2,△ABC的面积S△ABC=3,求a.
(本小题满分12分)如图,已知椭圆C: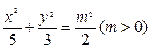 ,经过椭圆C的右焦点F且斜率为k(k≠0)的直线l交椭圆C于A、B两点,M为线段AB的中点,设O为椭圆的中心,射线OM交椭圆于N点.(1)是否存在k,使对任意m>0,总有
,经过椭圆C的右焦点F且斜率为k(k≠0)的直线l交椭圆C于A、B两点,M为线段AB的中点,设O为椭圆的中心,射线OM交椭圆于N点.(1)是否存在k,使对任意m>0,总有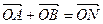 成立?若存在,求出所有k的值;
成立?若存在,求出所有k的值;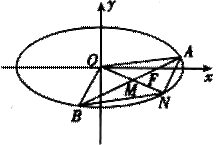 (2)若
(2)若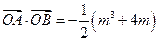 ,求实数k的取值范围.
,求实数k的取值范围.
(本小题满分12分)已知函数 (Ⅰ)求
(Ⅰ)求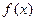 的极值;(Ⅱ)若函数
的极值;(Ⅱ)若函数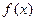 的图象与函数
的图象与函数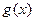 =1的图象在区间
=1的图象在区间 上有公共点,求实数a的取值范围.
上有公共点,求实数a的取值范围.