第 届亚运会于
届亚运会于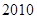 年
年 月
月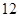 日至
日至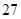 日在中国广州进行,为了做好接待工作,组委会招募了
日在中国广州进行,为了做好接待工作,组委会招募了 名男志愿者和
名男志愿者和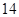 名女志愿者,调查发现,男、女志愿者中分别有
名女志愿者,调查发现,男、女志愿者中分别有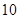 人和
人和 人喜爱运动,其余不喜爱.
人喜爱运动,其余不喜爱.
根据以上数据完成以下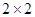 列联表:
列联表:
| |
喜爱运动 |
不喜爱运动 |
总计 |
| 男 |
10 |
|
16 |
| 女 |
6 |
|
14 |
| 总计 |
|
|
30 |
(2)能否在犯错误的概率不超过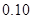 的前提下认为性别与喜爱运动有关?
的前提下认为性别与喜爱运动有关?
(3)如果从喜欢运动的女志愿者中(其中恰有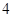 人会外语),抽取
人会外语),抽取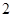 名负责翻译工作,则抽出的志愿者中
名负责翻译工作,则抽出的志愿者中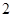 人都能胜任翻译工作的概率是多少?
人都能胜任翻译工作的概率是多少?
附:K2=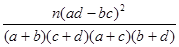
| P(K2≥k) |
0.100 |
0.050 |
0.025 |
0.010 |
0.001 |
| k |
2.706 |
3.841 |
5.024 |
6.635 |
10.828 |
(本小题满分12分) 已知关于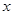 的不等式
的不等式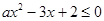 的解集为
的解集为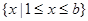 .
.
(1)求实数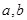 的值;
的值;
(2)解关于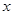 的不等式:
的不等式: (
( 为常数).
为常数).
(本小题满分10分)已知命题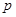 :方程
:方程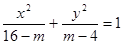 表示焦点在
表示焦点在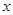 轴上的椭圆;命题
轴上的椭圆;命题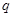 :点
:点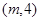 在圆
在圆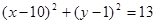 内.若
内.若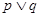 为真命题,
为真命题,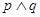 为假命题,试求实数
为假命题,试求实数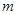 的取值范围.
的取值范围.
已知椭圆C: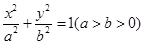 的两焦点与短轴的一个端点的连线构成等腰直角三角形,直线
的两焦点与短轴的一个端点的连线构成等腰直角三角形,直线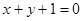 与以椭圆C的右焦点为圆心,以
与以椭圆C的右焦点为圆心,以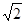
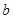 为半径的圆相切.
为半径的圆相切.
(1)求椭圆的方程.
(2)若过椭圆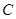 的右焦点
的右焦点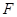 作直线
作直线 交椭圆
交椭圆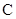 于
于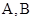 两点,交y轴于
两点,交y轴于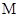 点,且
点,且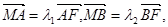 求证:
求证: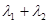 为定值
为定值
(本小题满分13分)(理科做)在如图所示的多面体中,底面BCFE是梯形,EF//BC,又EF 平面AEB,AE
平面AEB,AE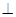 EB,AD//EF,BC=2AD=4,EF=3,AE=BE=2,G为BC的中点.
EB,AD//EF,BC=2AD=4,EF=3,AE=BE=2,G为BC的中点.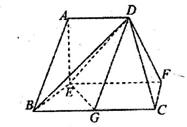
(1)求证:AB//平面DEG;
(2)求证:BD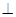 EG;
EG;
(3)求二面角C—DF—E的正弦值.
(文科做)已知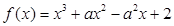 .
.
(1)若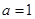 ,求曲线
,求曲线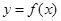 在点
在点 处的切线方程;
处的切线方程;
(2)若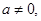 求函数
求函数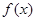 的单调区间.
的单调区间.
(本小题满分8分)已知圆C: ,直线
,直线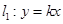 与圆C交于P、Q两个不同的点,M为P、Q的中点.
与圆C交于P、Q两个不同的点,M为P、Q的中点.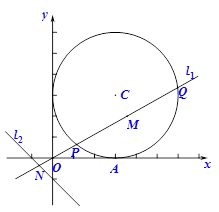
(Ⅰ)已知 ,若
,若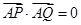 ,求实数
,求实数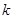 的值;
的值;
(Ⅱ)求点M的轨迹方程;