在直角坐标系
中以
为极点,
轴正半轴为极轴建立坐标系.圆
,直线
的极坐标方程分别为
.
(I)求
交点的极坐标.
(II)设
为
的圆心,为
交点连线的中点,已知直线
的参数方程为
(
为参数),求
的值.
设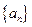 是一个公差为
是一个公差为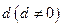 的等差数列,它的前
的等差数列,它的前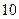 项和
项和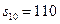 且
且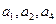 成等比数列,(1)证明
成等比数列,(1)证明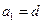 ;(2)求公差
;(2)求公差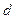 的值和数列
的值和数列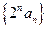 的前
的前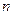 项和
项和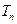 .
.
设函数
.
(Ⅰ)求
的最小正周期.
(Ⅱ)若函数
与
的图像关于直线
对称,求当
时
的最大值.
某单位为绿化环境,移栽了甲、乙两种大树各2株.设甲、乙两种大树移栽的成活率分别为
和
,且各株大树是否成活互不影响.求移栽的4株大树中:
(Ⅰ)两种大树各成活1株的概率;
(Ⅱ)成活的株数
的分布列与期望.
已知椭圆C
的离心率为
,过右焦点
的直线
与
相交于
两点,当
的斜率为1是,坐标原点
到直线
的距离为
.
(Ⅰ)求
的值;
(Ⅱ)
上是否存在点
,使得当
绕
转到某一位置时,有
成立?
若存在,求出所有的P的坐标与
的方程;若不存在,说明理由.
设函数 ,其中常数 .
(Ⅰ)讨论
的单调性;
(Ⅱ)若当
时,
恒成立,求
的取值范围.