某校为了解高三年级不同性别的学生对体育课改上自习课的态度(肯定还是否定),进行了如下的调查研究.全年级共有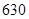 名学生,男女生人数之比为
名学生,男女生人数之比为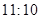 ,现按分层抽样方法抽取若干名学生,每人被抽到的概率均为
,现按分层抽样方法抽取若干名学生,每人被抽到的概率均为 .
.
(1)求抽取的男学生人数和女学生人数;
(2)通过对被抽取的学生的问卷调查,得到如下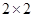 列联表:
列联表:
| |
否定 |
肯定 |
总计 |
| 男生 |
|
10 |
|
| 女生 |
30 |
|
|
| 总计 |
|
|
|
①完成列联表;
②能否有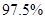 的把握认为态度与性别有关?
的把握认为态度与性别有关?
(3)若一班有 名男生被抽到,其中
名男生被抽到,其中 人持否定态度,
人持否定态度,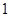 人持肯定态度;二班有
人持肯定态度;二班有 名女生被抽到,其中
名女生被抽到,其中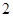 人持否定态度,
人持否定态度,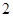 人持肯定态度.
人持肯定态度.
现从这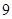 人中随机抽取一男一女进一步询问所持态度的原因,求其中恰有一人持肯定态度一人持否定态度的概率.
人中随机抽取一男一女进一步询问所持态度的原因,求其中恰有一人持肯定态度一人持否定态度的概率.
解答时可参考下面临界值表:
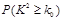 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
(本题满分12分)
已知函数 的零点为
的零点为 ,
,
(1)试求 的值;
的值;
(2)解不等式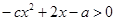 。
。
(本小题满分13分)
函数 ,数列
,数列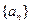 和
和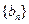 满足:
满足: ,
,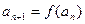 ,函数
,函数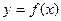 的图像在点
的图像在点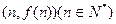 处的切线在
处的切线在 轴上的截距为
轴上的截距为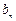 .
.
(1)求数列{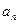 }的通项公式;
}的通项公式;
(2)若数列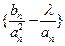 的项中仅
的项中仅 最小,求
最小,求 的取值范围;
的取值范围;
(3)若函数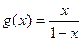 ,令函数
,令函数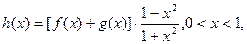 数列
数列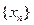 满足:
满足: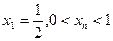 且
且 证明:
证明: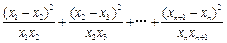
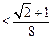 .
.
(本小题满分13分)
已知函数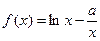 ,
,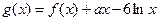 ,其中
,其中 R.
R.
(1)当a=1时,判断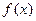 的单调性;
的单调性;
(2)若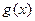 在其定义域内为增函数,求正实数
在其定义域内为增函数,求正实数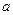 的取值范围;
的取值范围;
(3)设函数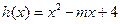 ,当
,当 时,若
时,若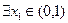 ,
,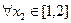 ,总有
,总有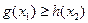 成立,求实数
成立,求实数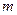 的取值范围.
的取值范围.
(本小题满分13分)
提高过江大桥的车辆通行能力可改善整个城市的交通状况.在一般情况下,大桥上的车
流速度v(单位:千米/小时)是车流密度 x(单位:辆/千米)的函数.当桥上的车流密度达
到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速
度为60千米/小时.研究表明当20≤x≤200时,车流速度v是车流密度x的一次函数.
(1)当0≤x≤200时,求函数v(x)的表达式;
(2)当车流密度x为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)f(x)=x·v(x)可以达到最大,并求出最大值.(精确到1辆/小时)
(本小题满分12分)
已知数列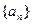 满足条件:
满足条件: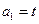 ,
,
(1)判断数列 是否为等比数列;
是否为等比数列;
(2)若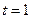 ,令
,令 , 记
, 记
证明:(ⅰ)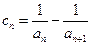 ;(ⅱ)
;(ⅱ)