已知四棱锥 的底面为直角梯形,
的底面为直角梯形, ,
, 底面
底面 ,且
,且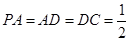 ,
,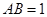 ,
, 是
是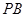 的中点。
的中点。
(Ⅰ)证明:面 面
面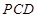 ;
;
(Ⅱ)求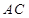 与
与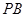 所成的角;
所成的角;
(Ⅲ)求面 与面
与面 所成二面角的大小。
所成二面角的大小。
为了让学生了解更多“奥运会”知识,某中学举行了一次“奥运知识竞赛”,共有800名学生参加了这次竞赛,为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计。请你根据表中信息解答下列问题:
(1)若用系统抽样的方法抽取容量为50的一个样本,则写出表中的①②③④⑤填的数据;
(2)作出频率分布直方图;
(3)试估计参加这次竞赛的学生的平均成绩
| 分组 |
频数 |
频率 |
| 60.5~70.5 |
① |
0.16 |
| 70.5~80.5 |
10 |
② |
| 80.5~90.5 |
18 |
0.36 |
90.5~100. 5 5 |
③ |
④ |
| 合计 |
50 |
⑤ |
(1)一本300页的书,随机打开一页,求页码在 之间的概率。
之间的概率。
(2)在区间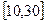 内的所有实数中,随机地取一个实数
内的所有实数中,随机地取一个实数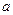 ,求实数
,求实数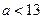 的概率
的概率
已知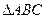 的3个顶点为
的3个顶点为 ,
, ,
,
(1)求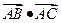 的值;
的值;
(2)求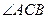 的大小,并判断
的大小,并判断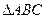 的形状。
的形状。
(本小题满分14分)
已知函数 (
(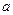 >0)的图象在点
>0)的图象在点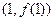 处的切线方程为
处的切线方程为 .
.
(Ⅰ)用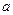 表示
表示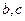 ;
;
(Ⅱ)若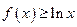 在
在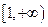 上恒成立,求
上恒成立,求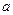 的取值范围;
的取值范围;
(Ⅲ)证明:1+ +
+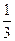 +…+
+…+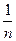 >
>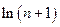 +
+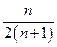
 .
.
(本小题满分14分)
在平面直角坐标系 中,设点
中,设点 (1,0),直线
(1,0),直线 :
: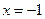 ,点
,点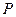 在直线
在直线 上移动,
上移动, 是线段
是线段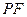 与
与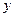 轴的交点,
轴的交点, 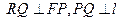 .
.
(Ⅰ)求动点 的轨迹方程;
的轨迹方程;
(Ⅱ) 记 的轨迹方程为
的轨迹方程为 ,过点
,过点 作两条互相垂直的曲线
作两条互相垂直的曲线 的弦
的弦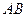 、
、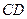 ,设
,设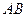 、
、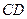 的中点分别为
的中点分别为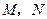 .求证:直线
.求证:直线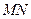 必过定点
必过定点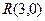 .
.