为了降低能源损耗,某城市对新建住宅的屋顶和外墙都要求建造隔热层.某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元.该建筑物每年的能源消耗费用C(单位:万元)与隔热层厚度 (单位:cm)满足关系:
(单位:cm)满足关系: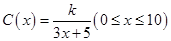 ,若不建隔热层,每年能源消耗费用为8万元.设
,若不建隔热层,每年能源消耗费用为8万元.设 为隔热层建造费用与20年的能源消耗费用之和.
为隔热层建造费用与20年的能源消耗费用之和.
(1)求 的值及
的值及 的表达式;
的表达式;
(2)隔热层修建多厚时,总费用 达到最小,并求最小值.
达到最小,并求最小值.
(本小题满分12分)设全集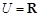 ,集合
,集合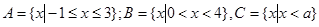
(1)求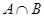 ,
,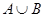 ;
;
(2)若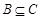 ,求实数
,求实数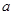 的取值范围.
的取值范围.
(本小题满分14分)一片森林原面积为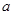 ,计划每年砍伐一些树,且每年砍伐面积的百分比相等,计划砍伐到面积一半时,所用时间是10年,为保护生态环境,森林面积至少要保留原面积的
,计划每年砍伐一些树,且每年砍伐面积的百分比相等,计划砍伐到面积一半时,所用时间是10年,为保护生态环境,森林面积至少要保留原面积的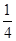 ,已知到今年为止,森林剩余面积为原的
,已知到今年为止,森林剩余面积为原的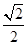 .
.
(1)求每年砍伐面积的百分比;
(2)到今年为止,该森林已砍伐了多少年;
(3)今后最多还能砍伐多少年?
(本小题满分13分)已知函数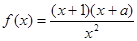 为偶函数.
为偶函数.
(1)求实数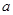 的值;
的值;
(2)记集合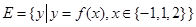 ,
,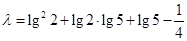 ,判断
,判断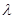 与
与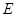 的关系;
的关系;
(3)当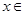
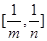
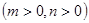 时,若函数
时,若函数 的值域为
的值域为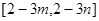 ,求
,求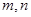 的值.
的值.
(本小题满分12分) 是定义在
是定义在 上的减函数,满足
上的减函数,满足 .
.
(1)求证: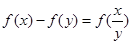 ;
;
(2)若 ,解不等式
,解不等式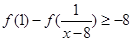 .
.
(本小题满分12分)已知函数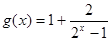 .
.
(1)用定义证明函数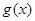 在
在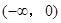 上为减函数.
上为减函数.
(2)求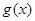 在
在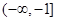 上的最小值.
上的最小值.