如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使DC=CB,延长DA
与⊙O的另一个交点为E,连结AC,CE。
(1)求证:∠B=∠D;
(2)若AB=4,BC-AC=2,求CE的长。
如图1,有一组平行线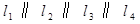 ,正方形
,正方形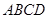 的四个顶点分别在
的四个顶点分别在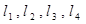 上,
上,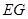 过点D且垂直于
过点D且垂直于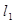 于点E,分别交
于点E,分别交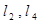 于点F,G,
于点F,G,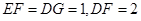 .
.
(1)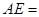 ,正方形
,正方形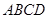 的边长=;
的边长=;
(2)如图2,将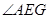 绕点A顺时针旋转得到
绕点A顺时针旋转得到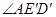 ,旋转角为
,旋转角为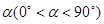 ,点
,点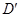 在直线
在直线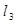 上,以
上,以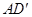 为边在的
为边在的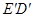 左侧作菱形
左侧作菱形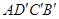 ,使点
,使点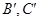 分别在直线
分别在直线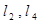 上.
上.
①写出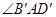 与
与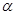 的函数关系并给出证明;②若
的函数关系并给出证明;②若 ,求菱形
,求菱形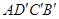 的边长.
的边长.
如图所示,在Rt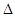 ABC中,∠C=90°,∠BAC=60°,AB=8.半径为
ABC中,∠C=90°,∠BAC=60°,AB=8.半径为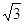 的⊙M与射线BA相切,切点为N,且AN=3.将Rt
的⊙M与射线BA相切,切点为N,且AN=3.将Rt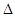 ABC顺时针旋转120
ABC顺时针旋转120 后得到Rt
后得到Rt ADE,点B、C的对应点分别是点D、E.
ADE,点B、C的对应点分别是点D、E.
(1)画出旋转后的Rt ADE;
ADE;
(2)求出Rt ADE的直角边DE被⊙M截得的弦PQ的长度;
ADE的直角边DE被⊙M截得的弦PQ的长度;
(3)判断Rt ADE的斜边AD所在的直线与⊙M的位置关系,并说明理由.
ADE的斜边AD所在的直线与⊙M的位置关系,并说明理由.
某宾馆有50个房间供游客住宿,当每个房间的房价为每天180元时,房间会全部住满.当每个房间每天的房价每增加10元时,就会有一个房间空闲.宾馆需对游客居住的每个房间每天支出20元的各种费用.根据规定,每个房间每天的房价不得高于340元.设每个房间的房价增加x元(x为10的正整数倍).
(1)设一天订住的房间数为y,直接写出y与x的函数关系式及自变量x的取值范围;
(2)设宾馆一天的利润为w元,求w与x的函数关系式;
(3)一天订住多少个房间时,宾馆的利润最大?最大利润是多少元?
如图,在矩形ABCD中,E,F为BC上两点,且BE=CF,连接AF,DE交于点O.求证: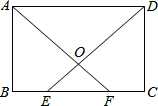
(1)△ABF≌△DCE;
(2)△AOD是等腰三角形.
如图,在△ABC中,∠C=90°, AD是∠BAC的平分线,O是AB上一点, 以 OA为半径的⊙O经过点D。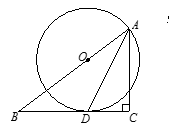
(1)求证: BC是⊙O切线;
(2)若BD="5," DC="3," 求AC的长。