过点
的圆C与直线
相切于点
.
（1）求圆C的方程；
（2）已知点
的坐标为
，设
分别是直线
和圆
上的动点，求
的最小值．
（3）在圆C上是否存在两点
关于直线
对称，且以
为直径的圆经过原点？若存在，写出直线的方程；若不存在，说明理由.
（本小题满分10分）在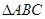
中，内角A、B、C的对边分别为
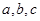，向量
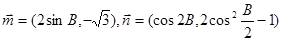，且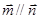
（1）求锐角B的大小；
（2）已知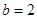
，求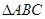的面积的最大值。
已知函数
．
（1）当
时，求
在
处的切线方程；
（2）设函数
，
（ⅰ）若函数
有且仅有一个零点时，求
的值；
（ⅱ）在（ⅰ）的条件下，若
，
，求
的取值范围。
已知向量
．
（1）当
时，求
的值；
（2）设函数
，已知在△ ABC中，内角A、B、C的对边分别为
，若
,求
（
）的取值范围．
已知首项都是1的两个数列{an}，{bn}（bn≠0，n∈N*）
满足anbn＋1－an＋1bn＋2bn＋1bn＝0．
（1）令cn＝
，求数列{cn}的通项公式；
（2）若bn＝3n－1，求数列{an}的前n项和Sn．
已知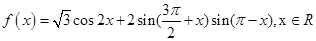
（1）最小正周期及对称轴方程；
（2）已知锐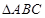角
的内角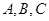
的对边分别为
,且 
,
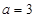,求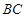
边上的高的最大值．