在△ABC中,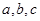 分别为三个内角
分别为三个内角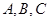 的对边,锐角
的对边,锐角 满足
满足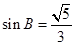 . (Ⅰ)求
. (Ⅰ)求 的值;
的值;
(Ⅱ) 若 ,当
,当 取最大值时,求
取最大值时,求 的值.
的值.
一个几何体是由圆柱 和三棱锥
和三棱锥 组合而成,点
组合而成,点 、
、 、
、 在圆
在圆 的圆周上,其正(主)视图、侧(左)视图的面积分别为10和12,如图4所示,其中
的圆周上,其正(主)视图、侧(左)视图的面积分别为10和12,如图4所示,其中 ,
, ,
, ,
, .
.
(1)求证: ;
;
(2)求三棱锥 的体积.
的体积.
为了了解某年段1000名学生的百米成绩情况,随机抽取了若干学生的百米成绩,成绩全部介于13秒与18秒之间,将成绩按如下方式分成五组:第一组[13,14);第二组[14,15);……;第五组[17,18].按上述分组方法得到的频率分布直方图如图3所示,已知图中从左到右的前3个组的频率之比为3∶8∶19,且第二组的频数为8.
(1)将频率当作概率,请估计该年段学生中百米成绩在[16,17)内的人数;
(2)求调查中随机抽取了多少个学生的百米成绩;
(3)若从第一、五组中随机取出两个成绩,求这两个成绩的差的绝对值大于1秒的概率.
已知函数 .
.
(1)求函数 的最小正周期和值域;
的最小正周期和值域;
(2)若函数 的图象过点
的图象过点 ,
, .求
.求 的值.
的值.
已知函数 ,
, ,
, 图象与
图象与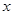 轴异于原点的交点M处的切线为
轴异于原点的交点M处的切线为 ,
,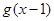 与
与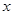 轴的交点N处的切线为
轴的交点N处的切线为 , 并且
, 并且 与
与 平行.
平行.
(1)求 的值;
的值;
(2)已知实数t∈R,求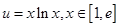 的取值范围及函数
的取值范围及函数 的最小值;
的最小值;
(3)令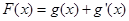 ,给定
,给定 ,对于两个大于1的正数
,对于两个大于1的正数 ,存在实数
,存在实数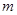 满足:
满足: ,
, ,并且使得不等式
,并且使得不等式 恒成立,求实数
恒成立,求实数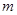 的取值范围.
的取值范围.
已知各项均为正数的数列 满足
满足 , 且
, 且 ,其中
,其中 .
.
(1) 求数列 的通项公式;
的通项公式;
(2) 设数列 满足
满足 ,是否存在正整数
,是否存在正整数 ,使得
,使得 成等比数列?若存在,求出所有的
成等比数列?若存在,求出所有的 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
(3) 令 ,记数列
,记数列 的前
的前 项和为
项和为 ,其中
,其中 ,证明:
,证明: 。
。