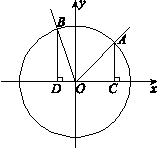
如图,在直角坐标系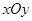 中,角
中,角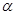 的顶点是原点,始边与
的顶点是原点,始边与 轴正半轴重合,终边交单位圆于点
轴正半轴重合,终边交单位圆于点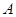 ,且
,且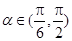 .将角
.将角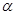 的终边按逆时针方向旋转
的终边按逆时针方向旋转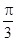 ,交单位圆于点
,交单位圆于点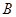 .记
.记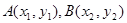 .
.
(Ⅰ)若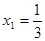 ,求
,求 ;
;
(Ⅱ)分别过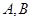 作
作 轴的垂线,垂足依次为
轴的垂线,垂足依次为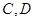 .记△
.记△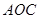 的面积为
的面积为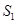 ,△
,△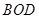 的面积为
的面积为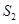 .若
.若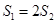 ,求角
,求角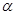 的值.
的值.
已知函数 ,设
,设
(1)求 的单调区间;
的单调区间;
(2)若以 图象上任意一点
图象上任意一点 为切点的切线的斜率
为切点的切线的斜率 恒成立,求实数
恒成立,求实数 的最小值;
的最小值;
(3)是否存在实数 ,使得函数
,使得函数 的图象与
的图象与 的图象恰好有四个不同的交点?若存在,求出
的图象恰好有四个不同的交点?若存在,求出 的取值范围,若不存在,说明理由。
的取值范围,若不存在,说明理由。
已知曲线  在点
在点 处的切线
处的切线  平行直线
平行直线 ,且点
,且点 在第三象限.
在第三象限.
(1)求 的坐标;
的坐标;
(2)若直线  , 且
, 且  也过切点
也过切点 ,求直线
,求直线 的方程.
的方程.
已知圆C: 内有一点P(2,2),过点P作直线
内有一点P(2,2),过点P作直线 交圆C于A、B两点。
交圆C于A、B两点。
(1)当 经过圆心C时,求直线
经过圆心C时,求直线 的方程;
的方程;
(2)当弦AB的长为 时,写出直线
时,写出直线 的方程。
的方程。
已知函数 .
.
(1)求曲线 在点
在点 处的切线方程;
处的切线方程;
(2)直线 为曲线
为曲线 的切线,且经过原点,求直线
的切线,且经过原点,求直线 的方程及切点坐标.
的方程及切点坐标.
已知:以点C (t,  )(t∈R , t ≠ 0)为圆心的圆与
)(t∈R , t ≠ 0)为圆心的圆与 轴交于点O, A,与y轴交于点O, B,其中O为原点.
轴交于点O, A,与y轴交于点O, B,其中O为原点.
(1)求证:△OAB的面积为定值;
(2)设直线y = –2x+4与圆C交于点M, N,若|OM| = |ON|,求圆C的方程.