已知函数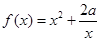
．
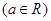(Ⅰ)若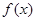
在
处的切线垂直于直线
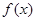，求该点的切线方程，并求此时函数的单调区间；
(Ⅱ)若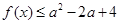
对任意的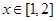
恒成立，求实数
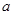的取值范围．
设函数
为奇函数，其图象在x=1处的切线与直线
垂直，导函数
的最小值为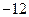
．
（I）求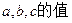
；
（II）求函数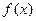
的单调递增区间，并求函数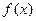在
上的最大值和最小值．
如图，已知矩形ABCD中，AB=10，BC=6，将矩形沿对角线BD把△ABD折起，使A移到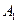
点，且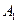在平面BCD上的射影O恰好在CD上．
（1）、求证：
；
（2）、求证：平面
平面
；
（3）、求三棱锥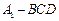
的体积．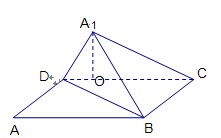 
已知平面向量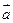
，
.
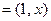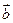
（Ⅰ）若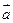⊥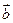，求x的值；
（Ⅱ）若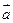∥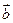，求|-|.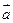
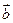已知函数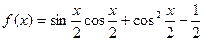
.
（Ⅰ）若
；
（Ⅱ）求函数
在
上最大值和最小值.
设函数f(x)＝xn（n≥2，n∈N*）
（1）若Fn(x)＝f(x－a)＋f(b－x)（0＜a＜x＜b），求Fn(x)的取值范围；
（2）若Fn(x)＝f(x－b)－f(x－a)，对任意n≥a (2≥a＞b＞0)，
证明：F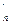
(n)≥n(a－b)(n－b)n-2。