已知 是椭圆
是椭圆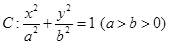 的右焦点,圆
的右焦点,圆 与
与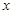 轴交于
轴交于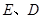 两点,
两点, 是椭圆
是椭圆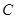 与圆
与圆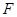 的一个交点,且
的一个交点,且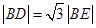 .
.
(Ⅰ)求椭圆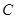 的离心率;
的离心率;
(Ⅱ)过点 与圆
与圆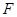 相切的直线
相切的直线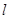 与
与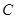 的另一交点为
的另一交点为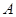 ,且
,且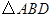 的面积等于
的面积等于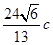 ,求椭圆
,求椭圆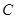 的方程.
的方程.
为了提高产品的年产量,某企业拟在2010年进行技术改革.经调查测算,产品当年的产量x万件与投入技术改革费用m万元(m≥0)满足x=3-(k为常数).如果不搞技术改革,则该产品当年的产量只能是1万件.已知2010年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元.由于市场行情较好,厂家生产的产品均能销售出去.厂家将每件产品的销售价格定为每件产品生产成本的1.5倍(生产成本包括固定投入和再投入两部分资金).
(1)将2010年该产品的利润y万元(利润=销售金额-生产成本-技术改革费用)表示为技术改革费用m万元的函数;
(2)该企业2010年的技术改革费用投入多少万元时,厂家的利润最大?
已知数列{an}的前n项和为Sn,点(n,)在直线y=x+上.数列{bn}满足bn+2-2bn+1+bn=0(n∈N*),b3=11,且其前9项和为153.
(1)求数列{an},{bn}的通项公式;
(2)设cn=,数列{cn}的前n项和为Tn,求使不等式Tn>对一切n∈N*都成立的最大正整数k的值.
在△ABC中,BC=,AC=3,sin C=2sin A.
(1)求AB的值;
(2)求sin的值.
(本题满分12分12分)设a,b∈R+,a+b=1.
(1)证明:ab+ ≥4+
≥4+ =4
=4 ;
;
(2)探索、猜想,将结果填在括号内;
a2b2+ ≥( _________ );a3b3+
≥( _________ );a3b3+ ≥( _________ );
≥( _________ );
(3)由(1)(2)你能归纳出更一般的结论吗?请证明你得出的结论.
设函数 ,其中
,其中 。
。
(Ⅰ)当 时,求不等式
时,求不等式 的解集;
的解集;
(Ⅱ)若不等式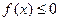 的解集为
的解集为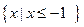 ,求a的值。
,求a的值。