设函数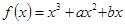 的图像在
的图像在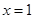 处取得极值4.
处取得极值4.
(1)求函数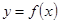 的单调区间;
的单调区间;
(2)对于函数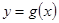 ,若存在两个不等正数
,若存在两个不等正数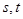
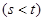 ,当
,当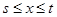 时,函数
时,函数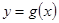 的值域是
的值域是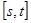 ,则把区间
,则把区间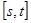 叫函数
叫函数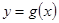 的“正保值区间”.问函数
的“正保值区间”.问函数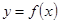 是否存在“正保值区间”,若存在,求出所有的“正保值区间”;若不存在,请说明理由.
是否存在“正保值区间”,若存在,求出所有的“正保值区间”;若不存在,请说明理由.
(1)将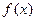 写成
写成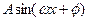 的形式,并求其图象对称中心的横坐标;
的形式,并求其图象对称中心的横坐标;
(2)如果△ABC的三边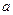 、
、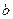 、
、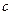 满足
满足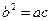 ,且边
,且边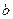 所对的角为
所对的角为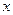 ,试求角
,试求角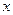 的范围及此时函数
的范围及此时函数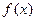 的值域
的值域
椭圆的离心率为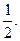 点
点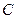 在
在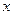 轴上,
轴上,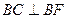 ,且
,且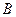 、
、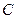 、
、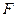 三点确定的圆
三点确定的圆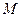 恰好与直线
恰好与直线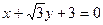 相切.
相切.
(Ⅰ)求椭圆的方程;
(Ⅱ)过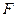 作一条与两坐标轴都不垂直的直线
作一条与两坐标轴都不垂直的直线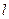 交椭圆于
交椭圆于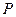 、
、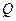 两点,在
两点,在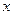 轴上是否存在定点
轴上是否存在定点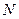 ,使得
,使得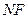 恰好为△
恰好为△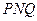 的内角平分线,若存在,求出点
的内角平分线,若存在,求出点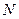 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.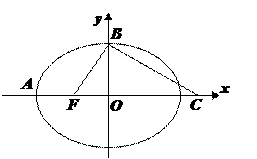
已知函数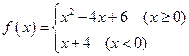 ,求不等式
,求不等式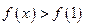 的解集.
的解集.
已知直线 ,直线
,直线 经过点
经过点 且与
且与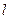 的夹角等于45°,求直线
的夹角等于45°,求直线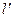 的一般方程.
的一般方程.
已知两点 和
和 分别在直线
分别在直线 和
和 上运动,且
上运动,且 ,动点满足:
,动点满足: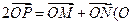 为坐标原点),点的轨迹记为曲线
为坐标原点),点的轨迹记为曲线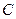
(1)求曲线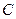 的方程,并讨论曲线
的方程,并讨论曲线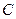 的类型;
的类型;
(2)过点(0,1)作直线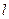 与曲线。交于不同的两点、,若对于任意
与曲线。交于不同的两点、,若对于任意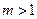 ,都有
,都有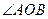 为锐角,求直线
为锐角,求直线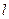 的斜率
的斜率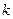 的取值范围。
的取值范围。