已知两点 和
和 分别在直线
分别在直线 和
和 上运动,且
上运动,且 ,动点满足:
,动点满足: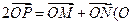 为坐标原点),点的轨迹记为曲线
为坐标原点),点的轨迹记为曲线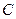
(1)求曲线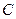 的方程,并讨论曲线
的方程,并讨论曲线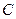 的类型;
的类型;
(2)过点(0,1)作直线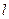 与曲线。交于不同的两点、,若对于任意
与曲线。交于不同的两点、,若对于任意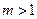 ,都有
,都有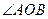 为锐角,求直线
为锐角,求直线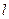 的斜率
的斜率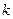 的取值范围。
的取值范围。
已知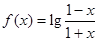 .
.
(1)求函数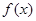 的定义域;
的定义域;
(2)判断并证明函数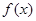 的奇偶性;
的奇偶性;
(3)若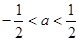 ,试比较
,试比较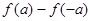 与
与 的大小.
的大小.
如图,在三棱柱ABC-A1B1C1中, CC1⊥底面ABC,AC=BC,M,N分别是CC1,AB的中点.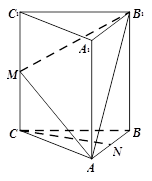
(1)求证:CN⊥AB1;
(2)求证:CN//平面AB1M.
设p;函数 在
在 上是增函数,q:函数
上是增函数,q:函数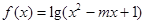 的定义域为R.
的定义域为R.
(1)若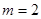 ,试判断命题p的真假;
,试判断命题p的真假;
(2)若命题p与命题q一真一假,试求实数 的取值范围.
的取值范围.
已知函数 ,其中常数
,其中常数 .
.
(1)求 的单调区间;
的单调区间;
(2)如果函数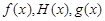 在公共定义域D上,满足
在公共定义域D上,满足 ,那么就称
,那么就称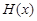 为
为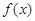 与
与 的“和谐函数”.设
的“和谐函数”.设 ,求证:当
,求证:当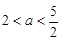 时,在区间
时,在区间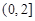 上,函数
上,函数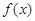 与
与 的“和谐函数”有无穷多个.
的“和谐函数”有无穷多个.
如图,椭圆 的离心率为
的离心率为 ,
, 轴被曲线
轴被曲线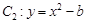 截得的线段长等于
截得的线段长等于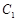 的短轴长。
的短轴长。 与
与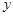 轴的交点为
轴的交点为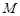 ,过坐标原点
,过坐标原点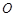 的直线
的直线 与
与 相交于点
相交于点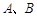 ,直线
,直线 分别与
分别与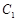 相交于点
相交于点 。
。
(1)求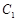 、
、 的方程;
的方程;
(2)求证: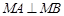 。
。
(3)记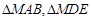 的面积分别为
的面积分别为 ,若
,若 ,求
,求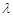 的取值范围。
的取值范围。