为了调查某大学学生在周日上网的时间，随机对名男生和名女生进行了不记名的问卷调查,得到了如下的统计结果：
表1：男生上网时间与频数分布表

上网时间（分钟）
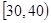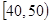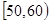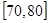人数	5	25	30	25	15

表2：女生上网时间与频数分布表

上网时间（分钟）
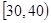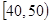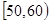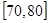人数	10	20	40	20	10

（Ⅰ）若该大学共有女生750人,试估计其中上网时间不少于60分钟的人数；
（Ⅱ）完成表3的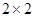列联表，并回答能否有90%的把握认为“学生周日上网时间与性别有关”？
（Ⅲ）从表3的男生中“上网时间少于60分钟”和“上网时间不少于60分钟”的人数中用分层抽样的方法抽取一个容量为5的样本，再从中任取两人，求至少有一人上网时间超过60分钟的概率.
表3 ：

	上网时间少于60分钟	上网时间不少于60分钟	合计
男生
女生
合计

附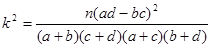：，其中

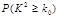	0.50	0.40	0.25	0.15	0.10	0.05	0.025	0.010	0.005	0.001
	0.455	0.708	1.323	2.072	2.706	3.84	5.024	6.635	7.879	10.83

 

科目 数学   题型 解答题   难度 中等