如图.在平面直角坐标系中,边长为 的正方形ABCD的顶点A、B在x轴上,连接OD、BD、△BOD的外心I在中线BF上,BF与AD交于点E.
的正方形ABCD的顶点A、B在x轴上,连接OD、BD、△BOD的外心I在中线BF上,BF与AD交于点E.
(1)求证:△OAD≌△EAB;
(2)求过点O、E、B的抛物线所表示的二次函数解析式;
(3)在(2)中的抛物线上是否存在点P,其关于直线BF的对称点在x轴上?若有,求出点P的坐标;
(4)连接OE,若点M是直线BF上的一动点,且△BMD与△OED相似,求点M的坐标.
.我市准备挑选一名跳高运动员参加省中学生运动会,对跳高队的甲、乙两名运动员进行了8次选拔比赛,他们的成绩(单位:cm)如下:
甲:170 165 168 169 172 173 168 167
乙:163 174 173 162 163 171 170 176
⑴甲、乙两名运动员的跳高平均成绩分别是多少?
⑵哪名运动员的成绩更为稳定?为什么?
⑶若预测,跳过165cm就很可能获得冠军.该校为了获得冠军,可能选哪位运动员参赛?为什么?若预测跳过170cm才能得冠军,可能选哪位运动员参赛?为什么?
已知:如图,AB=AC,点D是BC的中点,AD=AE,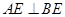 ,垂足为E.
,垂足为E.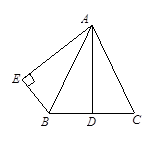 则∠BAC=2∠BAE,请说明理由.
则∠BAC=2∠BAE,请说明理由.
(本题6分) 如图,已知∠1+∠2=180°,∠DEF=∠A,试判断∠ACB与∠DEB的大小关系,
并对结论进行说明.
(本题6分) 如图,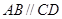 ,
,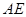 平分
平分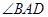 ,
,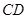 与
与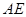 相交于点
相交于点 ,
,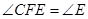 。试说明:
。试说明: 。
。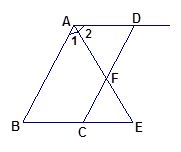
如图,已知: ,
,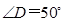 ,求
,求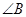 的度数。
的度数。