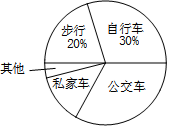
某中学为了解全校学生到校上学的方式,在全校随机抽取了若干名学生进行问卷调查.问卷给出了五种上学方式供学生选择,每人只能选一项,且不能不选.同时把调查得到的结果绘制成如图所示的条形统计图和扇形统计图(均不完整).请根据图中提供的信息解答下列问题: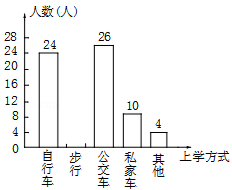
(1)在这次调查中,一共抽取了多少名学生?
(2)通过计算补全条形统计图;
(3)在扇形统计图中,“公交车”部分所对应的圆心角是多少度?
(4)若全校有1600名学生,估计该校乘坐私家车上学的学生约有多少名?
已知二次函数 的图象与 轴的交于 、 两点,与 轴交于点 ,
(1)求二次函数的表达式及 点坐标;
(2) 是二次函数图象上位于第三象限内的点,求点 到直线 的距离取得最大值时点 的坐标;
(3) 是二次函数图象对称轴上的点,在二次函数图象上是否存在点 ,使以 、 、 、 为顶点的四边形是平行四边形?若有,请写出点 的坐标(不写求解过程).

如图,四边形 内接于圆, ,对角线 平分 .
(1)求证: 是等边三角形;
(2)过点 作 交 的延长线于点 ,若 , ,求 的面积.

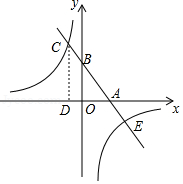
如图,一次函数 、 为常数, 的图象与 轴、 轴分别交于 、 两点,且与反比例函数 为常数且 的图象在第二象限交于点 , 轴,垂足为 ,若 .
(1)求一次函数与反比例函数的解析式;
(2)求两个函数图象的另一个交点 的坐标;
(3)请观察图象,直接写出不等式 的解集.
如图,已知边长为10的正方形 , 是 边上一动点(与 、 不重合),连结 , 是 延长线上的点,过点 作 的垂线交 的角平分线于点 ,若 .
(1)求证: ;
(2)若 ,求 的面积;
(3)请直接写出 为何值时, 的面积最大.

某班级为践行“绿水青山就是金山银山”的理念,开展植树活动.如果每人种3棵,则剩86棵;如果每人种5棵,则最后一人有树种但不足3棵.请问该班有多少学生?本次一共种植多少棵树?(请用一元一次不等式组解答)