在平面直角坐标系xOy中，一次函数y=2x+2的图象与x轴交于A，与y轴交于点C，点B的坐标为（a，0），（其中a＞0），直线l过动点M（0，m）（0＜m＜2），且与x轴平行，并与直线AC、BC分别相交于点D、E，P点在y轴上（P点异于C点）满足PE=CE，直线PD与x轴交于点Q，连接PA．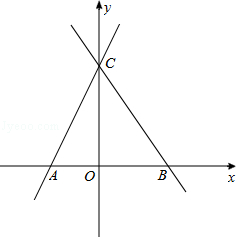
（1）写出A、C两点的坐标；
（2）当0＜m＜1时，若△PAQ是以P为顶点的倍边三角形（注：若△HNK满足HN=2HK，则称△HNK为以H为顶点的倍边三角形），求出m的值；
（3）当1＜m＜2时，是否存在实数m，使CD•AQ=PQ•DE？若能，求出m的值（用含a的代数式表示）；若不能，请说明理由．
解方程：⑴
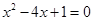（用配方法⑵
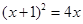
(本题12分)△ABC中，∠A，∠B，∠C的对边分别为a，b，c，关于x的方程x2－2ax＋b2=0的两根为x1、x2，x轴上两点M、N的坐标分别为（x1，0）、（x2，0），其中M的坐标是(a＋c，0)；P是y轴上一点，点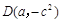
。
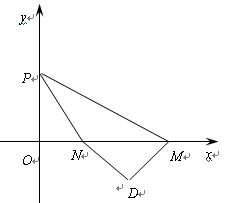
(1)试判断△ABC的形状，并说明理由；
(
2)若S△MNP＝3S△NOP，①求sinB的值； ②判断△ABC的三边长能否取一组适当的值，使△
MND是等腰直角三角形？如能，请求出这组值；如不能，请说明理由．
（本题12分）如图甲，两个不全等的等腰直角三角形OAB和OCD叠放在一起，并且有公共的直角顶点O.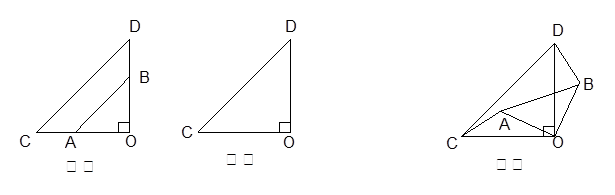
（1）在图甲中，你发现线段AC、BD的数量关系是_______，直线AC、BD相交成____度角；
（2）将图甲中的
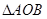绕点O顺时针旋转
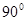，在图乙中作出旋转后的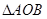；（3）将图甲中的
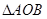绕点O顺时针旋转一个锐角，得到图丙，这时（1）中的两个结论是否成立？作出判断，并说明理由.若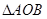绕点O继续旋转更大的角度时，结论仍然成立吗？作出判断，不必说明理由.
（本题10分）食品厂生产的
一种巧克力糖每千克成本为24元，其销售方案有如下两种：
方案1若直接给本厂设在某地的门市部销售，则每千克售价为32元，但门市部每月需要有关费用2400元。
方案2若直接批发给超市销售，则出厂价为每千克28元。
若每月只能按一种方案销售，且每种方案都能按月销售完当月产品，设该厂每月的销售量为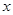
千克。（1）如果你是厂长，应该如何选择销售方案，可使工厂当月所获利润更大？
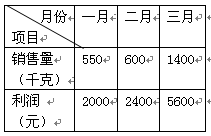
（2）厂长看到会计送来的第一季度销售量与利润关系的报表（如下表）后，发现该表填写的销售量与实际有不符之处，请找出不符之处，并计算第一季度的实际销售总量
（本题8分）小唐同学正在操场上放风筝，风筝从A处起飞，几分钟后便飞达C处，此时，在AQ延长线上B处的小宋同学，发现自己的位置与风筝和旗杆PQ的顶点P在同一直线上.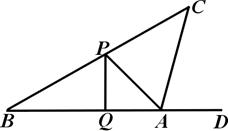
（1）已知旗杆高为10米，若在B处测得旗杆顶点P的仰角为30°，A处测得点P的仰角为45°，试求A、B之间的距离；
（2）此时，在A处背向旗杆又测得风筝的仰角为75°，若绳子在空中视为一条线段，求绳子AC约为多少？（结果保留根号）