为了解某市今年初二年级男生的身体素质状况,从该市初二年级男生中抽取了一部分学生进行“掷实心球”的项目测试.成绩低于6米为不合格,成绩在6至8米(含6米不含8米)的为及格,成绩在8米至12米(含8米和12米,假定该市初二学生掷实心球均不超过12米)为优秀.把获得的所有数据,分成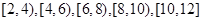 五组,画出的频率分布直方图如图所示.已知有4名学生的成绩在10米到12米之间.
五组,画出的频率分布直方图如图所示.已知有4名学生的成绩在10米到12米之间.
(Ⅰ)求实数 的值及参加“掷实心球”项目测试的人数;
的值及参加“掷实心球”项目测试的人数;
(Ⅱ)根据此次测试成绩的结果,试估计从该市初二年级男生中任意选取一人,“掷实心球”成绩为优秀的概率;
(Ⅲ)若从此次测试成绩不合格的男生中随机抽取2名学生再进行其它项目的测试,求所抽取的2名学生来自不同组的概率.
已知各项均为正数的数列{a }满足a
}满足a =2a
=2a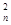 +a
+a a
a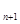 ,且a
,且a +a
+a =2a
=2a +4,其中n∈N
+4,其中n∈N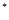 .
.
(Ⅰ)若b =
= ,求数列{b
,求数列{b }的通项公式;
}的通项公式;
(Ⅱ)证明: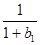 +
+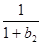 +…+
+…+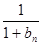 >
>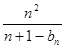 (n≥2).
(n≥2).
如图,已知椭圆C: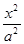 +
+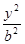 =1(a>b>0)的左、右焦点分别为F
=1(a>b>0)的左、右焦点分别为F 、F
、F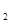 ,A是椭圆C上的一点,AF
,A是椭圆C上的一点,AF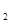 ⊥F
⊥F F
F ,O是坐标原点,OB垂直AF
,O是坐标原点,OB垂直AF 于B,且OF
于B,且OF =3OB.
=3OB.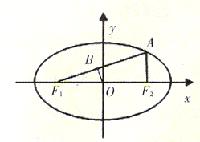
(Ⅰ)求椭圆C的离心率;
(Ⅱ)求t∈(0,b),使得命题“设圆x +y
+y =t
=t 上任意点M(x
上任意点M(x ,y
,y )处的切线交椭圆C于Q
)处的切线交椭圆C于Q 、Q
、Q 两点,那么OQ
两点,那么OQ ⊥OQ
⊥OQ ”成立.
”成立.
已知函数f(x)=x|x-a|-lnx,a∈R.
(Ⅰ)若a=1,求函数f(x)在区间[1,e]上的最大值;
(Ⅱ)若f(x)>0恒成立,求a的取值范围.
如图,三棱柱ABC-A B
B C
C 的侧面A
的侧面A ACC
ACC 与底面ABC垂直,AB=BC=CA=4,且AA
与底面ABC垂直,AB=BC=CA=4,且AA ⊥A
⊥A C,AA
C,AA =A
=A C.
C.
(Ⅰ)证明:AC⊥BA ;
;
(Ⅱ)求侧面A ABB
ABB 与底面ABC所成二面角的余弦值.
与底面ABC所成二面角的余弦值.
在某国际高端经济论坛上,前六位发言的是与会的含有甲、乙的6名中国经济学专家,他们的发言顺序通过随机抽签方式决定.
(Ⅰ)求甲、乙两位专家恰好排在前两位出场的概率;
(Ⅱ)发言中甲、乙两位专家之间的中国专家数记为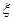 ,求
,求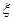 的分布列和数学期望.
的分布列和数学期望.