某饮料公司对一名员工进行测试以便确定其考评级别.公司准备了两种不同的饮料共5 杯,其颜色完全相同,并且其中3杯为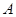 饮料,另外2杯为
饮料,另外2杯为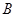 饮料,公司要求此员工一一品尝后,从5杯饮料中选出3杯
饮料,公司要求此员工一一品尝后,从5杯饮料中选出3杯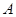 饮料.若该员工3杯都选对,则评为优秀;若3杯选对2杯,则评为良好;否则评为及格.假设此人对
饮料.若该员工3杯都选对,则评为优秀;若3杯选对2杯,则评为良好;否则评为及格.假设此人对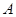 和
和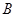 两种饮料没有鉴别能力.
两种饮料没有鉴别能力.
(Ⅰ)求此人被评为优秀的概率;
(Ⅱ)求此人被评为良好及以上的概率.
已知等差数列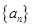 满足:
满足: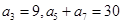 ,
,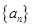 的前n项和为
的前n项和为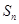 .
.
(1)求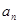 及
及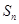 ;
;
(2)已知数列 的第n项为
的第n项为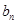 ,若
,若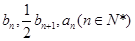 成等差数列,且
成等差数列,且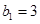 ,设数列
,设数列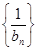 的前
的前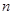 项和
项和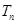 .求数列
.求数列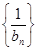 的前
的前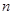 项和
项和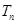 .
.
设有关于x的一元二次方程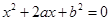 .
.
(1)若a是从0,1,2,3四个数中任取的一个数,b是从0,1,2三个数中任取的一个数,求上述方程有实根的概率;
(2)若a是从区间[0,3]任取的一个数,b是从区间[0,2]任取的一个数,求上述方程有实根的概率.
已知函数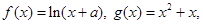 若函数
若函数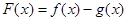 在x = 0处取得极值.
在x = 0处取得极值.
(1) 求实数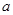 的值;
的值;
(2) 若关于x的方程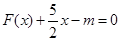 在区间[0,2]上恰有两个不同的实数根,求实数
在区间[0,2]上恰有两个不同的实数根,求实数 的取值范围;
的取值范围;
(3) 证明:对任意的自然数n,有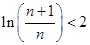 恒成立.
恒成立.
已知函数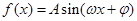 (其中
(其中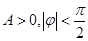 )的图象如图所示.
)的图象如图所示.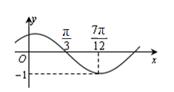
(1) 求函数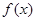 的解析式;
的解析式;
(2) 设函数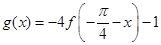 ,且
,且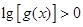 ,求
,求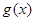 的单调区间.
的单调区间.
已知函数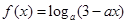 .
.
(1) 当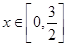 时,函数
时,函数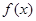 恒有意义,求实数a的取值范围;
恒有意义,求实数a的取值范围;
(2) 是否存在这样的实数a,使得函数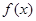 在区间
在区间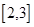 上为增函数,并且
上为增函数,并且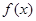 的最大值为1.如果存在,试求出a的值;如果不存在,请说明理由.
的最大值为1.如果存在,试求出a的值;如果不存在,请说明理由.