在三棱拄 中,
中,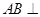 侧面
侧面 ,已知
,已知 ,
, ,
, .
.
(Ⅰ)求证: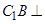 平面
平面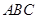 ;
;
(Ⅱ)试在棱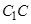 (不包含端点
(不包含端点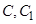 )上确定一点
)上确定一点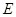 的位置,使得
的位置,使得 ;
;
(Ⅲ)在(Ⅱ)的条件下,求 和平面
和平面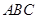 所成角正弦值的大小.
所成角正弦值的大小.
(本小题满分12分) 已知一个四棱锥的三视图如图所示,其中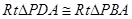 ,且
,且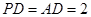 ,
,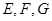 分别为
分别为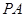 、
、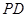 、
、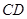 的中点
的中点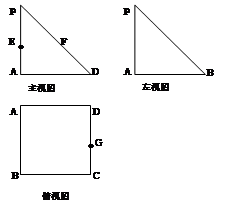
(1)求证:PB//平面EFG
(2)求直线PA与平面EFG所成角的大小
(3)在直线CD上是否存在一点Q,使二面角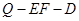 的大小为
的大小为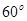 ?若存在,求出CQ的长;若不存在,请说明理由。
?若存在,求出CQ的长;若不存在,请说明理由。
(本小题满分12分)某校举行环保知识大奖赛,比赛分初赛和决赛两部分,初赛采用选手选一题答一题的方式进行,每位选手最多有5次选题答题的机会,选手累计答对3题或答错3题即终止其初赛的比赛,答对3题者直接进入决赛,答错3题者则被淘汰,已知选手甲答题连续两次答错的概率为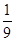 ,(已知甲回答每个问题的正确率相同,并且相互之间没有影响。)(I)求甲选手回答一个问题的正确率;(Ⅱ)求选手甲可进入决赛的概率;(Ⅲ)设选手甲在初赛中答题的个数为
,(已知甲回答每个问题的正确率相同,并且相互之间没有影响。)(I)求甲选手回答一个问题的正确率;(Ⅱ)求选手甲可进入决赛的概率;(Ⅲ)设选手甲在初赛中答题的个数为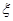 ,试写出
,试写出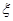 的分布列,并求
的分布列,并求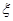 的数学期望。
的数学期望。
对数列{an},规定{△an}为数列{an}的一阶差分数列,其中 。
。
对自然数k,规定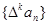 为{an}的k阶差分数列,其中
为{an}的k阶差分数列,其中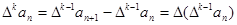 。
。
(1)已知数列{an}的通项公式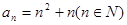 ,试判断
,试判断 是否为等差或等比数列,为什么?
是否为等差或等比数列,为什么?
(2)若数列{an}首项a1=1,且满足 ,求数列{an}的通项公式。
,求数列{an}的通项公式。
(3)对(2)中数列{an},是否存在等差数列{bn},使得 对一切自然
对一切自然 都成立?若存在,求数列{bn}的通项公式;若不存在,则请说明理由。
都成立?若存在,求数列{bn}的通项公式;若不存在,则请说明理由。
已知函数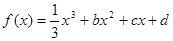 ,设曲线y=
,设曲线y= 在与x轴交点处的切线为y=4x-12,
在与x轴交点处的切线为y=4x-12,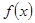 为
为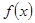 的导函数,且满足
的导函数,且满足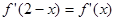
(1)求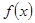
(2)设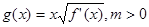 ,求函数g(x)在[0,m]上的最大值。
,求函数g(x)在[0,m]上的最大值。
(3)设 ,若对一切
,若对一切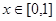 ,不等式
,不等式 恒成立,求实数t的取值范围
恒成立,求实数t的取值范围
已知函数 的定义域是
的定义域是 ,且满足
,且满足 ,
, ,如果对于0<x<y,都有
,如果对于0<x<y,都有 ,
,
(1)求 ;
;
(2)解不等式