某地区因干旱缺水,政府向市民宣传节约用水,并进行广泛动员 三个月后,统计部门在一个小区随机抽取了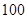 户家庭,分别调查了他们在政府动员前后三个月的月平均用水量(单位:吨),将所得数据分组,画出频率分布直方图(如图所示)
户家庭,分别调查了他们在政府动员前后三个月的月平均用水量(单位:吨),将所得数据分组,画出频率分布直方图(如图所示)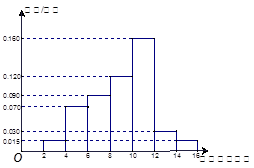

动员前 动员后
(Ⅰ)已知该小区共有居民 户,在政府进行节水动员前平均每月用水量是
户,在政府进行节水动员前平均每月用水量是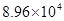 吨,请估计该小区在政府动员后比动员前平均每月节约用水多少吨;
吨,请估计该小区在政府动员后比动员前平均每月节约用水多少吨;
(Ⅱ)为了解动员前后市民的节水情况,媒体计划在上述家庭中,从政府动员前月均用水量在 范围内的家庭中选出
范围内的家庭中选出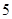 户作为采访对象,其中在
户作为采访对象,其中在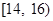 内的抽到
内的抽到 户,求
户,求 的分布列和期望
的分布列和期望
已知关于 的不等式
的不等式
 .
.
(Ⅰ)若不等式 的解集为
的解集为 ,求
,求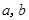 的值.
的值.
(Ⅱ)求不等式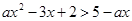
 的解集.
的解集.
某学校一个生物兴趣小组对学校的人工湖中养殖的某种鱼类进行观测研究,在饲料充足的前提下,兴趣小组对饲养时间x(单位:月)与这种鱼类的平均体重y(单位:千克)得到一组观测值,如下表:
 (月) (月) |
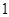 |
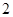 |
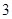 |
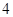 |
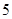 |
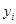 (千克) (千克) |
 |
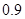 |
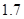 |
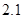 |
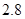 |
(1)在给出的坐标系中,画出关于x、y两个相关变量的散点图.
(2)请根据上表提供的数据,用最小二乘法求出变量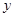 关于变量
关于变量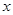 的线性回归直线方程
的线性回归直线方程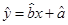 .
.
(3)预测饲养满12个月时,这种鱼的平均体重(单位:千克).
(参考公式: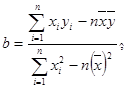 ,
,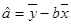 ,
,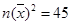 ,
,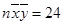 ,
,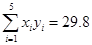 ,
,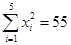
设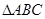 的内角
的内角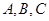 所对的边分别为
所对的边分别为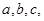 且
且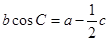 .
.
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)若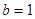 ,求
,求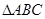 的周长
的周长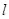 的取值范围.
的取值范围.
已知公差不为零的等差数列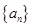 中,
中,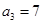 ,且
,且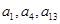 成等比数列.
成等比数列.
(Ⅰ)求数列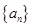 的通项公式;
的通项公式;
(Ⅱ)令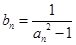 (
(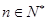 ),求数列
),求数列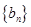 的前
的前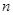 项和
项和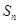 .
.
已知函数 的最小正周期为
的最小正周期为 .
.
(Ⅰ)求函数 的表达式并求
的表达式并求 在区间
在区间 上的最小值;
上的最小值;
(Ⅱ)在 中,
中, 分别为角
分别为角 所对的边,且
所对的边,且 ,
, ,求角
,求角 的大小.
的大小.