在直角坐标系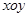 中,曲线
中,曲线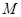 的参数方程为
的参数方程为 (
(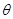 为参数),若以直角坐标系的原点
为参数),若以直角坐标系的原点 为极点,
为极点,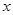 轴的正半轴为极轴建立极坐标,曲线
轴的正半轴为极轴建立极坐标,曲线 的极坐标方程为
的极坐标方程为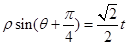 (其中
(其中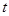 为常数).
为常数).
(1)若曲线 与曲线
与曲线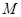 只有一个公共点,求
只有一个公共点,求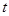 的取值范围;
的取值范围;
(2)当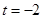 时,求曲线
时,求曲线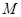 上的点与曲线
上的点与曲线 上的点的最小距离.
上的点的最小距离.
已知 的内角
的内角 的对边分别为
的对边分别为 ,且满足
,且满足 ,
, .
.
(1)求 的面积;
的面积;
(2)若 ,求
,求 的值.
的值.
已知两直线 和
和 ,试确定
,试确定 ,
, 的值,使(1)
的值,使(1) ;(2)
;(2) ,且
,且 在
在 轴上的截距为-1.
轴上的截距为-1.
已知数列 是首项为
是首项为 ,公比
,公比 的等比数列,
的等比数列,



 ,数列
,数列 满足
满足 .
.
(1)求证: 是等差数列;
是等差数列;
(2)求数列 的前
的前 项和
项和 ;
;
(3)若 对一切正整数
对一切正整数 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
4-5:不等式选讲(本小题满分10分)
设函数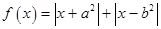 ,其中
,其中 ,
, 为实数.
为实数.
(1)若 ,解关于
,解关于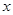 的不等式
的不等式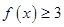 ;
;
(2)若 ,证明:
,证明: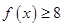
4-4:坐标系与参数方程(本小题满分10分)
在平面直角坐标系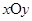 中,
中,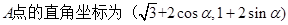 (
( 为参数).在以原点
为参数).在以原点 为极点,
为极点,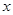 轴正半轴为极轴的极坐标中,直线
轴正半轴为极轴的极坐标中,直线 的极坐标方程为
的极坐标方程为 .
.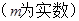 .
.
(1)试求
(2)设 点对应的轨迹为曲线
点对应的轨迹为曲线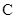 ,若曲线
,若曲线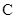 上存在四个点到直线
上存在四个点到直线 的距离为1,求实数
的距离为1,求实数 的取值范围.
的取值范围.