已知函数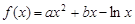 ,
,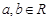 .
.
(1)若 且
且 ,试讨论
,试讨论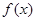 的单调性;
的单调性;
(2)若对 ,总
,总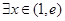 使得
使得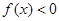 成立,求实数
成立,求实数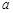 的取值范围.
的取值范围.
(本小题共12分)已知函数 .
.
(Ⅰ)若 是函数
是函数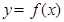 的极值点,求
的极值点,求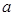 的值;
的值;
(Ⅱ)求函数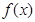 的单调区间.
的单调区间.
【改编题】(本小题满分12分)已知圆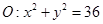 ,点
,点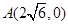 ,以线段AB为直径的圆内切于圆
,以线段AB为直径的圆内切于圆 ,记点B的轨迹为
,记点B的轨迹为 .
.
(Ⅰ)求曲线 的方程;
的方程;
(Ⅱ)若直线 (
( )与曲线
)与曲线 交于不同的两点
交于不同的两点 ,
,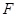 ,以线段
,以线段 为直径作圆
为直径作圆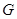 .若圆
.若圆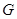 与
与 轴相切,求直线
轴相切,求直线 被圆
被圆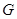 所截得的弦长..
所截得的弦长..
(本小题满分12分)某城市有东西南北四个进入城区主干道的入口,在早高峰时间段,时常发生交通拥堵现象,交警部门统计11月份30天内的拥堵天数,东西南北四个主干道入口的拥堵天数分别是18天,15天,9天,15天.假设每个入口发生拥堵现象互相独立,视频率为概率.
(1)求该城市一天中早高峰时间段恰有三个入口发生拥堵的概率;
(2)设 表示一天中早高峰时间段发生拥堵的主干道入口个数,求
表示一天中早高峰时间段发生拥堵的主干道入口个数,求 的分布列和数学期望.
的分布列和数学期望.
(本小题满分12分)如图,在四棱锥 中,底面
中,底面 是正方形,
是正方形, 底面
底面 ,
, ,点
,点 是
是 的中点,
的中点, 且交
且交 于点
于点 .
.
(Ⅰ)求证:平面 平面
平面 ;
;
(Ⅱ)求二面角 的余弦值.
的余弦值.
(本小题满分12分)已知函数 的图象经过点
的图象经过点 .
.
(Ⅰ)求 的值以及
的值以及 ;
;
(Ⅱ)函数 的图象向右平移
的图象向右平移 后得到函数
后得到函数 的图象,求
的图象,求 在
在 上的值域.
上的值域.