已知数列 的前
的前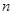 项和为
项和为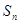 ,若
,若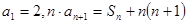 ,
,
⑴证明数列 为等差数列,并求其通项公式;
为等差数列,并求其通项公式;
⑵令 ,①当
,①当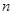 为何正整数值时,
为何正整数值时, :②若对一切正整数
:②若对一切正整数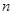 ,总有
,总有 ,求
,求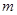 的取值范围.
的取值范围.
若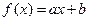 ,则
,则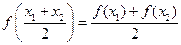 ;
;
学校举办运动会时,高一(1)班共有28名同学参加比赛,有15人参加游泳比赛,有8人参加田径比赛,有14人参加球类比赛,同时参加游泳比赛和田径比赛的有3人,同时参加游泳比赛和球类比赛的有3人,没有人同时参加三项比赛.问同时参加田径和球类比赛的有多少人?只参加游泳一项比赛的有多少人?

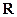 时,一次函数
时,一次函数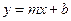 在
在 和
和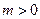 时的单调性是怎样的?利用函数单调性的定义证明你的结论.
时的单调性是怎样的?利用函数单调性的定义证明你的结论.
某服装厂生产一种服装,每件服装的成本为40元,出厂单价定为60元.该厂为鼓励销售商订购,决定当一次订购量超过100件时,每多订购一件,订购的全部服装的出厂单价就降低0.02元.根据市场调查,销售商一次订购量不会超过500件.
(1)设一次订购量为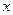 件,服装的实际出厂单价为
件,服装的实际出厂单价为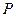 元,写出函数
元,写出函数 的表达式;
的表达式;
(2)当销售商一次订购了450件服装时,该服装厂获得的利润是多少元?
(服装厂售出一件服装的利润=实际出厂单价-成本).
已知 ,内有一动点P,
,内有一动点P, 于M,
于M, 于N,且四边形PMON的面积等于4,今以O为原点,
于N,且四边形PMON的面积等于4,今以O为原点, 的平分线
的平分线 为极轴(如图),求动点P的轨迹方程。
为极轴(如图),求动点P的轨迹方程。