已知数列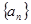 及其前
及其前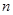 项和
项和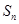 满足:
满足: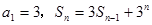 (
(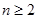 ,
, ).
).
(1)证明:设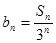 ,
,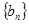 是等差数列;
是等差数列;
(2)求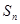 及
及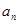 ;
;
(3)判断数列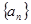 是否存在最大或最小项,若有则求出来,若没有请说明理由.
是否存在最大或最小项,若有则求出来,若没有请说明理由.
小波以游戏方式决定是去打球、唱歌还是去下棋。游戏规则为:以
为起点,再从
(如图)这六个点中任取两点分别为终点得到两个向量,记这两个向量的数量积为
,若
就去打球,若
就去唱歌,若
就去下棋。
(1)写出数量积
的所有可能值;
(2)分别求小波去下棋的概率和不去唱歌的概率。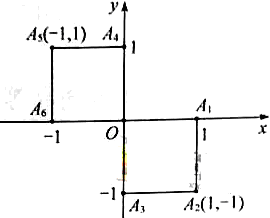
在 中,角 的对边分别是 ,已知 .
(1)求证: 成等差数列;
(2)若
,求
的值.
正项数列 .
如图,已知椭圆
与
的中心在坐标原点
,长轴均为
且在
轴上,短轴长分别为
,
,过原点且不与
轴重合的直线
与
的四个交点按纵坐标从大到小依次为
,记
,
和
的面积分别为
和
.
(1)当直线
与
轴重合时,若
,求
的值;
(2)当
变化时,是否存在与坐标轴不重合的直线
,使得
?并说明理由.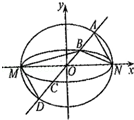
设
,已知函数
.
(Ⅰ)当
时,讨论函数
的单调性;
(Ⅱ)当
时,称
为
关于
的加权平均数.
(1)判断
是否成等比数列,并证明
;
(2)
的几何平均数记为
.称
为
的调和平均数,记为
.若
,求
的取值范围.