已知函数f(x)=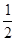 x
x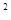 -ax+(a-1)
-ax+(a-1)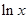 ,
,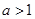 。
。
(1)讨论函数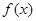 的单调性;(2)若
的单调性;(2)若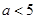 ,设
,设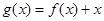 ,
,
(ⅰ)求证g(x)为单调递增函数;
(ⅱ)求证对任意x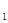 ,x
,x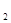
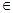
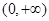 ,x
,x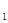
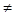 x
x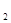 ,有
,有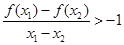 .
.
已知向量 ,
, ,若函数
,若函数 .
.
(1)求 的最小正周期;
的最小正周期;
(2)若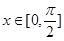 ,求
,求 的最大值及相应的
的最大值及相应的 值;
值;
(3)若 ,求
,求 的单调递减区间.
的单调递减区间.
在直角坐标系xOy中,直线l的方程为x﹣y+4=0,曲线C的参数方程为 (α为参数)已知在极坐标(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,点P的极坐标为(4,
(α为参数)已知在极坐标(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,点P的极坐标为(4, ),判断点P与直线l的位置关系;
),判断点P与直线l的位置关系;
(2)设点Q是曲线C上的一个动点,求它到直线l的距离的最小值.
已知函数f(x)=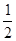
 -ax(a∈R,e为自然对数的底数).
-ax(a∈R,e为自然对数的底数).
(1)讨论函数f(x)的单调性;
(2)若a=1,函数g(x)=(x-m)f(x)-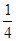
 +x2+x在区间(0,+
+x2+x在区间(0,+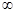 )上为增函数,求整数m 的最大值.
)上为增函数,求整数m 的最大值.
已知椭圆C:
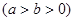 和直线L:
和直线L: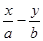 ="1," 椭圆的离心率
="1," 椭圆的离心率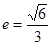 ,坐标原点到直线L的距离为
,坐标原点到直线L的距离为 。
。
(1)求椭圆的方程;
(2)已知定点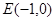 ,若直线
,若直线
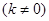 与椭圆C相交于M、N两点,试判断是否存在
与椭圆C相交于M、N两点,试判断是否存在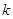 值,使以MN为直径的圆过定点E?若存在求出这个
值,使以MN为直径的圆过定点E?若存在求出这个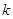 值,若不存在说明理由。
值,若不存在说明理由。
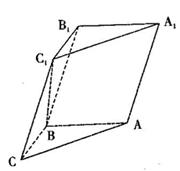
如图,在三棱柱ABC-A1B1C1中,已知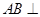 侧面
侧面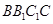 ,AB=BC=1,BB1=2,∠BCC1=
,AB=BC=1,BB1=2,∠BCC1=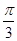 .
.
(1) 求证:C1B⊥平面ABC;
(2)设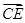 =l
=l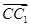 (0≤l≤1),且平面AB1E与BB1E所成的锐二面角
(0≤l≤1),且平面AB1E与BB1E所成的锐二面角
的大小为30°,试求l的值.