已知椭圆C:
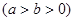 和直线L:
和直线L: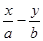 ="1," 椭圆的离心率
="1," 椭圆的离心率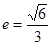 ,坐标原点到直线L的距离为
,坐标原点到直线L的距离为 。
。
(1)求椭圆的方程;
(2)已知定点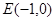 ,若直线
,若直线
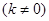 与椭圆C相交于M、N两点,试判断是否存在
与椭圆C相交于M、N两点,试判断是否存在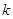 值,使以MN为直径的圆过定点E?若存在求出这个
值,使以MN为直径的圆过定点E?若存在求出这个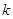 值,若不存在说明理由。
值,若不存在说明理由。
(本小题满分14分)已知函数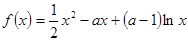
 .
.
(Ⅰ)讨论函数 的单调性;
的单调性;
(Ⅱ)若 ,数列
,数列 满足
满足 .
.
(1)若首项 ,证明数列
,证明数列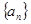 为递增数列;
为递增数列;
(2)若首项为正整数,且数列 为递增数列,求首项
为递增数列,求首项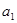 的最小值.
的最小值.
(本小题满分13分)如图,菱形 的边长为
的边长为 ,现将
,现将 沿对角线
沿对角线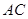 折起至
折起至 位置,并使平面
位置,并使平面 平面
平面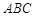 .
. 
(1)求证: ;
;
(2)在菱形 中,若
中,若 ,求直线
,求直线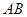 与平面
与平面 所成角的正弦值;
所成角的正弦值;
(3)求四面体 体积的最大值.
体积的最大值.
(本小题满分13分) 在平面直角坐标系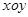 中,点
中,点 与点
与点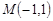 关于原点
关于原点 对称,
对称, 是动点,且直线
是动点,且直线 与
与 的斜率之积等于
的斜率之积等于 .
.
(1)求动点 的轨迹方程;
的轨迹方程;
(2)设直线 和
和 与直线
与直线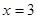 分别交于
分别交于 两点,问:是否存在点
两点,问:是否存在点 使得
使得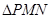 与
与 的面积相等?若存在,求出点
的面积相等?若存在,求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(本小题满分13分)某同学用“五点法”画函数 (
(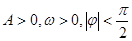 )在某一个周期内的图像时,列表并填入的部分数据如下表:
)在某一个周期内的图像时,列表并填入的部分数据如下表:
 |
 |
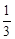 |
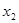 |
 |
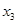 |
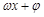 |
 |
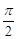 |
 |
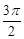 |
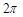 |
 |
 |
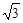 |
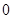 |
 |
 |
(1)请求出上表中的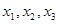 的值,并写出函数
的值,并写出函数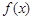 的解析式;
的解析式;
(2)将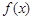 的图像向右平移
的图像向右平移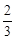 个单位得到函数
个单位得到函数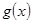 的图像,若函数
的图像,若函数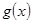 在区间
在区间 (
(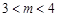 )上的图像的最高点和最低点分别为
)上的图像的最高点和最低点分别为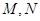 ,求向量
,求向量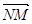 与
与 夹角
夹角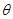 的大小.
的大小.
(本小题满分13分)甲、乙两支篮球队赛季总决赛采用7场4胜制,每场必须分出胜负,场与场之间互不影响,只要有一队获胜4场就结束比赛.现已比赛了4场,且甲篮球队胜3场.已知甲球队第5,6场获胜的概率均为 ,但由于体力原因,第7场获胜的概率为
,但由于体力原因,第7场获胜的概率为 .
.
(1)求甲队分别以 ,
, 获胜的概率;
获胜的概率;
(2)设X表示决出冠军时比赛的场数,求X的分布列及数学期望.