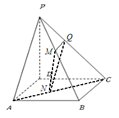
(本小题满分13分)某同学用“五点法”画函数 (
(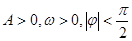 )在某一个周期内的图像时,列表并填入的部分数据如下表:
)在某一个周期内的图像时,列表并填入的部分数据如下表:
 |
 |
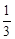 |
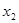 |
 |
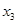 |
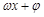 |
 |
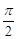 |
 |
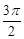 |
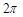 |
 |
 |
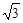 |
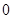 |
 |
 |
(1)请求出上表中的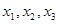 的值,并写出函数
的值,并写出函数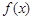 的解析式;
的解析式;
(2)将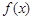 的图像向右平移
的图像向右平移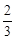 个单位得到函数
个单位得到函数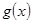 的图像,若函数
的图像,若函数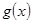 在区间
在区间 (
(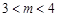 )上的图像的最高点和最低点分别为
)上的图像的最高点和最低点分别为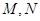 ,求向量
,求向量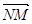 与
与 夹角
夹角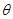 的大小.
的大小.
设数列 是公差大于0的等差数列,
是公差大于0的等差数列,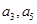 分别是方程
分别是方程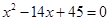 的两个实根
的两个实根
(1)求数列 的通项公式
的通项公式
(2)设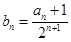 ,求数列
,求数列 的前
的前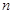 项和
项和
在 中,角
中,角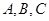 所对应的边分别为
所对应的边分别为 ,且
,且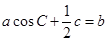
 ,
,
(1)求角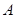 的大小
的大小
(2)若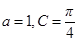 , 求
, 求 的面积
的面积
如图,圆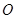 的直径
的直径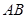 的延长线与弦
的延长线与弦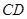 的延长线相交于点
的延长线相交于点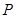 ,
,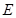 为圆
为圆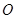 上一点,
上一点,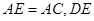 交
交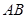 于点
于点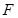 ,且
,且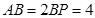
(1)求线段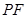 的长度
的长度
(2)若圆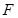 与圆
与圆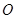 内切,直线
内切,直线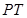 与圆
与圆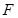 切于点
切于点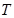 ,
,
求线段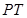 的长度
的长度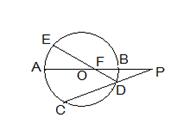
(本小题满分12分)如图,在正方体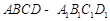 中,
中,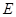 、
、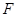 分别为棱
分别为棱 、
、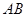 的中点.
的中点.
(1)求证:平面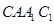 ⊥平面
⊥平面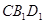 ;
;
(2)如果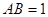 ,一个动点从点
,一个动点从点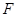 出发在正方体的表面上依次经过棱
出发在正方体的表面上依次经过棱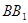 、
、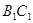 、
、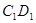 、
、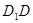 、
、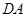 上的点,最终又回到点
上的点,最终又回到点 ,指出整个路线长度的最小值并说明理由.
,指出整个路线长度的最小值并说明理由.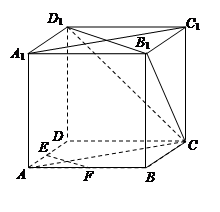
(本小题12分)如图,四棱锥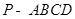 中,底面
中,底面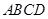 是正方形,
是正方形,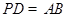 ,
, 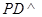 底面
底面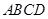 ,
,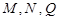 分别在
分别在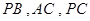 上,且
上,且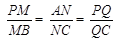
(1)求证:平面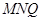 ∥平面
∥平面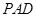 .
.
(2)求直线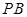 与平面面
与平面面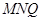 所成角的正弦值.
所成角的正弦值.