省少年篮球队要从甲、乙两所体校选拔队员。现将这两所体校共20名学生的身高绘制成如下茎叶图(单位:cm):若身高在180cm以上(包括180cm)定义为“高个子”,身高在180cm以下(不包括180cm)定义为“非高个子”.
(Ⅰ)用分层抽样的方法从“高个子”和“非高个子”中抽取5人,如果从这5人中随机选2人,那么至少有一人是“高个子”的概率是多少?
(Ⅱ)若从所有“高个子”中随机选3名队员,用 表示乙校中选出的“高个子”人数,试求出
表示乙校中选出的“高个子”人数,试求出 的分布列和数学期望.
的分布列和数学期望.
已知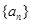 为等差数列,且
为等差数列,且 ,
,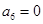 。
。
(1)求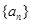 的通项公式;
的通项公式;
(2)若等比数列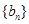 满足
满足 ,
,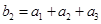 ,求
,求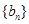 的前n项和公式.
的前n项和公式.
(本小题满分13分)
已知数列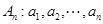
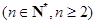 满足
满足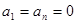 ,且当
,且当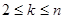
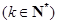 时,
时,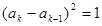 ,令
,令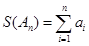 .
.
(Ⅰ)写出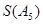 的所有可能的值;
的所有可能的值;
(Ⅱ)求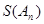 的最大值;
的最大值;
(Ⅲ)是否存在数列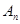 ,使得
,使得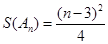 ?若存在,求出数列
?若存在,求出数列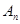 ;若不存在,说明理由.
;若不存在,说明理由.
(本小题满分13分)
在平面直角坐标系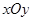 中,已知点
中,已知点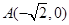 ,
,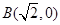 ,
,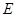 为动点,且直线
为动点,且直线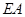 与直线
与直线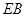 的斜率之积为
的斜率之积为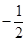 .
.
(Ⅰ)求动点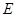 的轨迹
的轨迹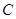 的方程;
的方程;
(Ⅱ)设过点 的直线
的直线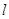 与曲线
与曲线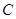 相交于不同的两点
相交于不同的两点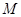 ,
,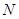 .若点
.若点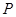 在
在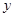 轴上,且<满足
轴上,且<满足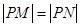 ,求点
,求点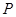 的纵坐标的取值范围.
的纵坐标的取值范围.
(本小题满分14分)
已知函数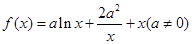 .
.
(Ⅰ)若曲线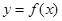 在点
在点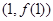 处的切线与直线
处的切线与直线 垂直,求实数
垂直,求实数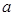 的值;
的值;
(Ⅱ)讨论函数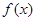 的单调性;
的单调性;
(Ⅲ)当 时,记函数
时,记函数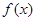 的最小值为
的最小值为 ,求证:
,求证: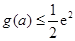 .
.
(本小题满分14分)
在如图所示的几何体中,四边形 为正方形,
为正方形, 平面
平面 ,
, ,
, .
.
(Ⅰ)若点 在线段
在线段 上,且满足
上,且满足 ,求证:
,求证: 平面
平面 ;
;
(Ⅱ)求证: 平面
平面 ;
;
(Ⅲ)求二面角 的余弦值.
的余弦值.