已知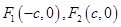 分别是椭圆
分别是椭圆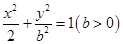 的左、右焦点,椭圆的离心率
的左、右焦点,椭圆的离心率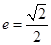 .
.
(I)求椭圆 的方程;(II)已知直线
的方程;(II)已知直线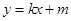 与椭圆
与椭圆 有且只有一个公共点
有且只有一个公共点 ,且与直线
,且与直线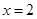 相交于点
相交于点 .求证:以线段
.求证:以线段 为直径的圆恒过定点
为直径的圆恒过定点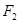 .
.
某校为进行爱国主义教育,在全校组织了一次有关钓鱼岛历史知识的竞赛.现有甲、乙两队参加钓鱼岛知识竞赛,每队3人,规定每人回答一个问题,答对为本队赢得1分,答错得0分.假设甲队中每人答对的概率均为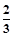 ,乙队中3人答对的概率分别为
,乙队中3人答对的概率分别为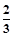 、
、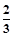 、
、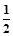 ,且各人回答正确与否相互之间没有影响,用ξ表示甲队的总得分.
,且各人回答正确与否相互之间没有影响,用ξ表示甲队的总得分.
(1)求随机变量ξ的分布列和数学期望;
(2)用A表示“甲、乙两个队总得分之和等于3”这一事件,用B表示“甲队总得分大于乙队总得分” 这一事件,求P(AB).
如图,在四棱柱ABCD—A1B1C1D1中,底面ABCD是等腰梯形,∠DAB=60°,AB=2 CD=2,M是线段AB的中点.
(1)求证:C1M∥平面A1ADD1 ;
(2)若CD1垂直于平面ABCD且CD1= ,求平面C1D1M和平面ABCD所成的角(锐角)的余弦值.
,求平面C1D1M和平面ABCD所成的角(锐角)的余弦值.
已知向量 ,
, ,函数f(x)=
,函数f(x)= ,且y=f(x)的图象过点
,且y=f(x)的图象过点 和点
和点 .
.
(1)求m,n的值;
(2)将y=f(x)的图象向左平移φ(0<φ<π)个单位后得到函数y=g(x)的图象,若y=g(x)图象上各最高点到点(0,3)的距离的最小值为1,求y=g(x)的单调递增区间.
选修4—5:不等式选讲
已知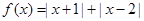 ,
,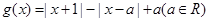 .
.
(Ⅰ)解不等式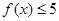 ;
;
(Ⅱ)若不等式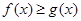 恒成立,求a的取值范围.
恒成立,求a的取值范围.
选修4—4:极坐标与参数方程
已知圆的极坐标方程为: .
.
(Ⅰ)将极坐标方程化为普通方程;并选择恰当的参数写出它的参数方程;
(Ⅱ)若点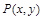 在该圆上,求
在该圆上,求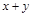 的最大值和最小值.
的最大值和最小值.