设 ,函数
,函数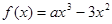 .
.
(1)若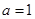 ,求函数
,求函数 的极值与单调区间;
的极值与单调区间;
(2)若函数 的图象在
的图象在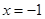 处的切线与直线
处的切线与直线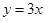 平行,求
平行,求 的值;
的值;
(3)若函数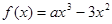 的图象与直线
的图象与直线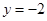 有三个公共点,求
有三个公共点,求 的取值范围.
的取值范围.
已知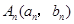 (
(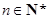 )是曲线
)是曲线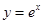 上的点,
上的点,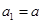 ,
,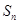 是数列
是数列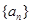 的前
的前 项和,且满足
项和,且满足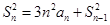 ,
,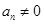 ,
,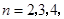 .
.
(1)证明:数列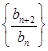 (
(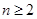 )是常数数列;
)是常数数列;
(2)确定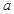 的取值集合
的取值集合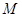 ,使
,使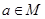 时,数列
时,数列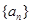 是单调递增数列;
是单调递增数列;
(3)证明:当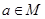 时,弦
时,弦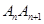 (
(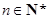 )的斜率随
)的斜率随 单调递增
单调递增
已知椭圆 的左右焦点分别为
的左右焦点分别为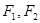 ,短轴两个端点为
,短轴两个端点为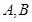 ,且四边形
,且四边形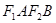 是边长为2的正方形.
是边长为2的正方形.
(1)求椭圆的方程;
(2)若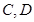 分别是椭圆长轴的左右端点,动点
分别是椭圆长轴的左右端点,动点 满足
满足 ,连接
,连接 ,交椭圆于点
,交椭圆于点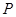 .证明:
.证明: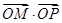 为定值;
为定值;
(3)在(2)的条件下,试问 轴上是否存在异于点
轴上是否存在异于点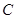 的定点
的定点 ,使得以
,使得以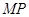 为直径的圆恒过直线
为直径的圆恒过直线 的交点,若存在,求出点
的交点,若存在,求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.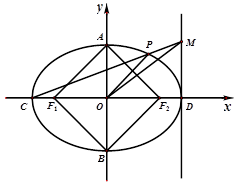
如图,某机场建在一个海湾的半岛上,飞机跑道AB的长为4.5km,且跑道所在的直线与海岸线l的夹角为60o(海岸线可以看作是直线),跑道上离海岸线距离最近的点B到海岸线的距离BC=4 km.D为海湾一侧海岸线CT上的一点,设CD=x(km),点D对跑道AB的视角为q.
km.D为海湾一侧海岸线CT上的一点,设CD=x(km),点D对跑道AB的视角为q.
(1)将tanq表示为x的函数;
(2)求点D的位置,使q取得最大值.
如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,四边形ABCD是平行四边形,且AC⊥CD,PA=AD,M,Q分别是PD,BC的中点.
(1)求证:MQ∥平面PAB;
(2)若AN⊥PC,垂足为N,求证:MN⊥PD.
已知函数 (
( ,
, 是实数常数)的图像上的一个最高点
是实数常数)的图像上的一个最高点 ,与该最高点最近的一个最低点是
,与该最高点最近的一个最低点是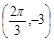 ,
,
(1)求函数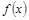 的解析式及其单调增区间;
的解析式及其单调增区间;
(2)在锐角三角形△ABC中,角A、B、C所对的边分别为 ,且
,且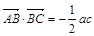 ,角A的取值范围是区间M,当
,角A的取值范围是区间M,当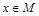 时,试求函数
时,试求函数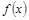 的取值范围.
的取值范围.