已知椭圆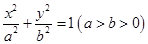 的离心率为
的离心率为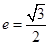 ,直线
,直线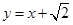 与以原点为圆心、椭圆
与以原点为圆心、椭圆 的短半轴长为半径的圆
的短半轴长为半径的圆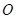 相切.
相切.
(1)求椭圆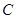 的方程;
的方程;
(2)如图,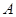 、
、 、
、 是椭圆
是椭圆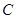 的顶点,
的顶点,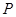 是椭圆
是椭圆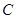 上除顶点外的任意点,直线
上除顶点外的任意点,直线 交
交 轴于点
轴于点 ,直线
,直线 交
交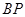 于点
于点 ,设
,设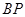 的斜率为
的斜率为 ,
, 的斜率为
的斜率为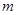 ,求证:
,求证: 为定值.
为定值.
在, 中,角A、B、C的对边分别为a、b、c, A=2B.
中,角A、B、C的对边分别为a、b、c, A=2B.
(I)若 ,求
,求 的值;
的值;
(II)若C为钝角,求 的取值范围.
的取值范围.
不等式选讲。
已知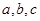 均为正实数,且
均为正实数,且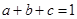 .求
.求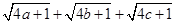 的最大值.
的最大值.
坐标系与参数方程
已知直线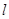 的极坐标方程是
的极坐标方程是 .以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,在曲线
.以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,在曲线 上求一点,使它到直线
上求一点,使它到直线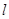 的距离最小,并求出该点坐标和最小距离.
的距离最小,并求出该点坐标和最小距离.
几何证明选讲。
如图,AB是⊙O的直径,弦BD、CA的延长线相交于点E,EF垂直BA的延长线于点F.
求证:(1)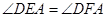 ;
;
(2)AB2=BE•BD-AE•AC.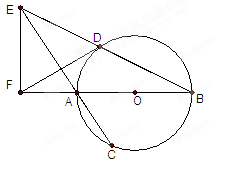
(本小题共12分)已知函数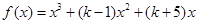 ,其中
,其中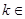
 .
.
(I)若函数 有三个不同零点,求
有三个不同零点,求 的取值范围;
的取值范围;
(II)若函数 在区间
在区间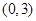 上不是单调函数,求
上不是单调函数,求 的取值范围.
的取值范围.