如图,已知四边形ABCD内接于 ,且AB是的
,且AB是的 直径,过点D的
直径,过点D的 的切线与BA的延长线交于点M.
的切线与BA的延长线交于点M.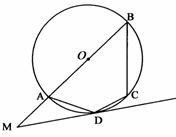
(1)若MD=6,MB=12,求AB的长;
(2)若AM=AD,求∠DCB的大小.
已知F1,F2是椭圆C: +
+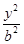 =1(a>b>0)的左、右焦点,点P(-
=1(a>b>0)的左、右焦点,点P(- ,1)在椭圆上,线段PF2与y轴的交点M满足
,1)在椭圆上,线段PF2与y轴的交点M满足 +
+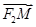 =0.
=0.
(1)求椭圆C的方程;
(2)椭圆C上任一动点N(x0,y0)关于直线y=2x的对称点为N1(x1,y1),求3x1-4y1的取值范围.
设椭圆E: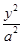 +
+ =1(a>b>0)的上焦点是F1,过点P(3,4)和F1作直线PF1交椭圆于A,B两点,已知A(
=1(a>b>0)的上焦点是F1,过点P(3,4)和F1作直线PF1交椭圆于A,B两点,已知A( ,
, ).
).
(1)求椭圆E的方程;
(2)设点C是椭圆E上到直线PF1距离最远的点,求C点的坐标.
设A,B分别为椭圆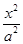 +
+ =1(a>b>0)的左、右顶点,(1,)为椭圆上一点,椭圆长半轴长等于焦距.
=1(a>b>0)的左、右顶点,(1,)为椭圆上一点,椭圆长半轴长等于焦距.
(1)求椭圆的方程;
(2)设P(4,x)(x≠0),若直线AP,BP分别与椭圆相交于异于A,B的点M,N,求证:∠MBN为钝角.
已知定义域为 的函数
的函数 同时满足以下三个条件:
同时满足以下三个条件:
①对任意的 ,总有
,总有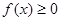 ;
;
② ;
;
③当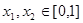 ,且
,且 时,
时,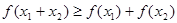 成立.
成立.
称这样的函数为“友谊函数”.
请解答下列各题:
(1)已知 为“友谊函数”,求
为“友谊函数”,求 的值;
的值;
(2)函数 在区间
在区间 上是否为“友谊函数”?请给出理由;
上是否为“友谊函数”?请给出理由;
(3)已知 为“友谊函数”,假定存在
为“友谊函数”,假定存在 ,使得
,使得 ,且
,且 ,求证:
,求证: .
.
已知线段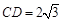 ,
,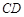 的中点为
的中点为 ,动点
,动点 满足
满足 (
(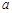 为正常数).
为正常数).
(1)建立适当的直角坐标系,求动点 所在的曲线方程;
所在的曲线方程;
(2)若 ,动点
,动点 满足
满足 ,且
,且 ,试求
,试求 面积的最大值和最小值.
面积的最大值和最小值.