已知函数 .
.
(1)若 在
在 处取得极大值,求实数
处取得极大值,求实数 的值;
的值;
(2)若 ,求
,求 在区间
在区间 上的最大值.
上的最大值.
已知f(x)=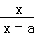 (x≠a).
(x≠a).
(1)若a=﹣2,试证f(x)在(﹣∞,﹣2)内单调递增;
(2)若a>0且f(x)在(1,+∞)内单调递减,求a的取值范围.
已知f(x)= (n∈Z).
(n∈Z).
(1)化简f(x)的表达式;
(2)求f( )+f(
)+f( π).
π).
已知集合M{h(x)|h(x)的定义域为R,且对任意x都有h(﹣x)=﹣h(x)}设函数f(x)= (a,b为常数).
(a,b为常数).
(1)当a=b=1时,判断是否有f(x)∈M,说明理由;
(2)若函数f(x)∈M,且对任意的x都有f(x)<sinθ成立,求θ的取值范围.
若在定义域内存在实数x0,使得f(x0+1)=f(x0)+f(1)成立,则称函数f(x)是“可拆函数”.
(1)函数f(x)= 是否是“可拆函数”?请说明理由;
是否是“可拆函数”?请说明理由;
(2)若函数f(x)=2x+b+2x是“可拆函数”,求实数b的取值范围:
(3)证明:f(x)=cosx是“可拆函数”.
如图,半径为4m的水轮绕着圆心O逆时针做匀速圆周运动,每分钟转动4圈,水轮圆心O距离水面2m,如果当水轮上点P从离开水面的时刻(P0)开始计算时间.
(1)将点P距离水面的高度y(m)与时间t(s)满足的函数关系;
(2)求点P第一次到达最高点需要的时间.