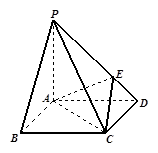己知函数 .
.
(I)若 是,
是, 的极值点,讨论
的极值点,讨论 的单调性;
的单调性;
(II)当 时,证明:
时,证明: .
.
已知向量 ,设函数
,设函数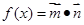 +
+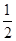 .(1)若
.(1)若 ,f(x)=
,f(x)= ,求
,求 的值;(2)在△ABC中,角A,B,C的对边分别是
的值;(2)在△ABC中,角A,B,C的对边分别是 ,且满足
,且满足 ,求f(B)的取值范围.
,求f(B)的取值范围.
已知函数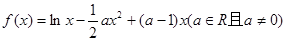 .
.
(1)求函数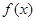 的单调递增区间;
的单调递增区间;
(2)记函数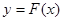 的图像为曲线
的图像为曲线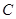 .设点
.设点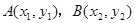 是曲线
是曲线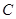 上不同两点.如果在曲线
上不同两点.如果在曲线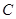 上存在点
上存在点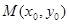 使得:①
使得:①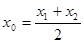 ;②曲线
;②曲线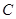 在点
在点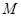 处的切线平行于直线
处的切线平行于直线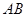 ,则称函数
,则称函数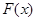 存在“中值相依切线”.
存在“中值相依切线”.
试问:函数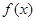 是否存在“中值相依切线”,请说明理由.
是否存在“中值相依切线”,请说明理由.
已知数列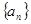 满足
满足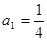 ,
, (
(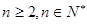 )。
)。
(1)求数列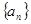 的通项公式;
的通项公式;
(2)设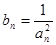 ,求
,求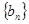 的前n项和
的前n项和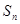 ;
;
(3)设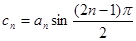 ,数列
,数列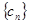 的前n项和
的前n项和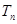 ,求证:对
,求证:对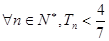 .
.
函数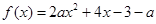 ,
, 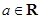 .
.
(1)当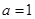 时,求函数
时,求函数 在
在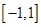 上的最大值;
上的最大值;
(2)如果函数 在区间
在区间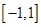 上存在零点,求
上存在零点,求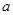 的取值范围.
的取值范围.
如图所示, 四棱锥P-ABCD的底面是边长为1的正方形,PA^CD,PA = 1,PD= ,E为PD上一点,PE = 2ED.
,E为PD上一点,PE = 2ED.
(1)求证:PA ^平面ABCD;
(2)求二面角D-AC-E的余弦值;
(3)在侧棱PC上是否存在一点F,使得BF // 平面AEC?
若存在,指出F点的位置,并证明;若不存在,说明理由.