已知函数f(x)的导函数为f ′(x),且对任意x>0,都有f ′(x)> .
.
(Ⅰ)判断函数F(x)= 在(0,+∞)上的单调性;
在(0,+∞)上的单调性;
(Ⅱ)设x1,x2∈(0,+∞),证明:f(x1)+f(x2)<f(x1+x2);
(Ⅲ)请将(Ⅱ)中的结论推广到一般形式,并证明你所推广的结论.
(1)(2005福建卷)已知函数 的图象在点M(-1,f(x))处的切线方程为x+2y+5=0.
的图象在点M(-1,f(x))处的切线方程为x+2y+5=0.
(Ⅰ)求函数y=f(x)的解析式;
已知函数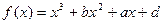 的图象过点P(0,2),且在点M(-1,f(-1))处的切线方程为
的图象过点P(0,2),且在点M(-1,f(-1))处的切线方程为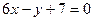 . (Ⅰ)求函数
. (Ⅰ)求函数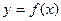 的解析式;
的解析式;
已知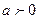 ,n为正整数。设
,n为正整数。设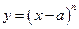 ,证明
,证明 ;
;
(1)设 ,对任意
,对任意 ,证明
,证明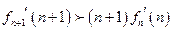
(1)(2005高考北京卷)已知函数f(x)=-x3+3x2+9x+a, (I)求f(x)的单调递减区间;(II)若f(x)在区间[-2,2]上的最大值为20,求它在该区间上的最小值.答案:(1)(-∞,-1),(3,+∞)(2)-7
( 2005全国卷III)已知函数 ,
,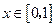 (Ⅰ)求
(Ⅰ)求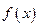 的单调区间和值域;
的单调区间和值域;
(Ⅱ)设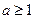 ,函数
,函数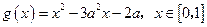 ,若对于任意
,若对于任意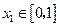 ,总存在
,总存在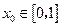 使得
使得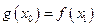 成立,求
成立,求 的取值范围。
的取值范围。