如图,AB是⊙O直径,D为⊙O上一点,AT平分∠BAD交⊙O于点T,过T作AD的垂线交AD的延长线于点C.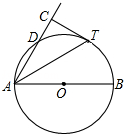
(1)求证:CT为⊙O的切线;
(2)若⊙O半径为2,CT=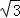 ,求AD的长.
,求AD的长.
如图,直线AE、CF分别被直线EF、AC所截,已知,∠1=∠2,AB平分∠EAC,CD平分∠ACG.将下列证明AB∥CD的过程及理由填写完整.
证明:∵ ∠1=∠2 (已知)
∴ AE∥()
∴∠EAC =∠,( )
而AB平分∠EAC,CD平分∠ACG( 已知 )
∴ ∠=  ∠EAC,∠4=
∠EAC,∠4=  ∠(角平分线的定义)
∠(角平分线的定义)
∴ ∠=∠4(等量代换)
∴ AB∥CD().
5个棱长为1的正方体组成如图的几何体.
(1)该几何体的体积是(立方单位),表面积是(平方单位);
(2)请在4×4网格图中画出该几何体的主视图和左视图.
如图,将两块直角三角尺的直角顶点O叠放在一起.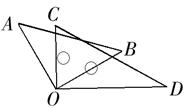
⑴若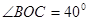 ,试求
,试求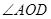 的度数.
的度数.
⑵若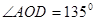 ,试求
,试求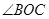 的度数.
的度数.
⑶若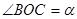 、
、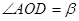 ,请写出
,请写出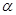 与
与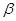 的大小关系式,并说明理由.
的大小关系式,并说明理由.
列方程解答:七年级某班举办迎元旦庆新年歌咏会,购买了一些笔记本作为纪念品,若参加表演的同学每人分3本,则剩6本;若参加表演的同学每人分4本,则还差2本,
问:⑴这个班共有多少名学生参加表演?
⑵购买的笔记本共有多少本?
如图,点O在直线AD上,∠EOC=90°,∠DOB=90°,若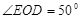 , 求∠AOC的度数
, 求∠AOC的度数