如图,抛物线 与
与 轴相交于点
轴相交于点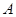 (﹣1,0)、
(﹣1,0)、 (3,0),与
(3,0),与 轴相交于点
轴相交于点 ,点
,点 为线段
为线段 上的动点(不与
上的动点(不与 、
、 重合),过点
重合),过点 垂直于
垂直于 轴的直线与抛物线及线段
轴的直线与抛物线及线段 分别交于点
分别交于点 、
、 ,点
,点 在
在 轴正半轴上,
轴正半轴上, =2,连接
=2,连接 、
、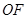 .
.
(1)求抛物线的解析式;
(2)当四边形 是平行四边形时,求点
是平行四边形时,求点 的坐标;
的坐标;
(3)过点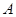 的直线将(2)中的平行四边形
的直线将(2)中的平行四边形 分成面积相等的两部分,求这条直线的解析式.(不必说明平分平行四边形面积的理由)
分成面积相等的两部分,求这条直线的解析式.(不必说明平分平行四边形面积的理由)
在2016年4月23日“世界读书日”之前,某校为了了解学生的阅读情况,对学生在2015年读课外书的数量进行了调查.所示图表是根据随机抽取的部分学生的读书数量情况整理的表格和两幅不完整的统计图,根据图中提供的信息,解答下列问题.
|
2015年学生的读书数量分组 |
||||
|
|
|
|
|
|
|
0 |
本 |
本 |
本 |
超过12本 |
(1)此次抽样调查共调查了 名学生?
(2)请将条形统计图补充完整;
(3)请说明样本数据中,学生读书数量的中位数落在哪个范围内;
(4)该校共有900名学生,估计在2015年读课外书的数量超过12本的学生有多少名?

如图,点 是平行四边形 的边 上一点,且 .
(1)作出 的平分线,交 于点 (尺规作图,不写作法,保留作图痕迹);
(2)连接 ,求证:四边形 是菱形.

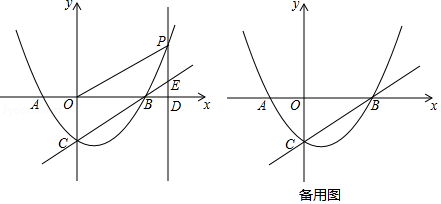
如图,抛物线 的对称轴是直线 ,与 轴交于 , 两点,与 轴交于点 ,点 的坐标为 ,点 为抛物线上的一个动点,过点 作 轴于点 ,交直线 于点 .
(1)求抛物线解析式;
(2)若点 在第一象限内,当 时,求四边形 的面积;
(3)在(2)的条件下,若点 为直线 上一点,点 为平面直角坐标系内一点,是否存在这样的点 和点 ,使得以点 , , , 为顶点的四边形是菱形?若存在,直接写出点 的坐标;若不存在,请说明理由.
【温馨提示:考生可以根据题意,在备用图中补充图形,以便探究】
在四边形 中,点 为 边上的一点,点 为对角线 上的一点,且 .
(1)若四边形 为正方形.
①如图1,请直接写出 与 的数量关系 ;
②将 绕点 逆时针旋转到图2所示的位置,连接 , ,猜想 与 的数量关系并说明理由;
(2)如图3,若四边形 为矩形, ,其它条件都不变,将 绕点 顺时针旋转 得到△ ,连接 , ,请在图3中画出草图,并直接写出 与 的数量关系.

夏季空调销售供不应求,某空调厂接到一份紧急订单,要求在10天内(含10天)完成任务.为提高生产效率,工厂加班加点,接到任务的第一天就生产了空调42台,以后每天生产的空调都比前一天多2台,由于机器损耗等原因,当日生产的空调数量达到50台后,每多生产一台,当天生产的所有空调,平均每台成本就增加20元.
(1)设第 天生产空调 台,直接写出 与 之间的函数解析式,并写出自变量 的取值范围.
(2)若每台空调的成本价(日生产量不超过50台时)为2000元,订购价格为每台2920元,设第 天的利润为 元,试求 与 之间的函数解析式,并求工厂哪一天获得的利润最大,最大利润是多少.