(阅读下面的题目及分析过程,并按要求进行证明.
已知:如图,E是BC的中点,点A在DE上,且∠BAE=∠CDE.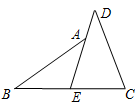
求证:AB=CD.
分析:证明两条线段相等,常用的一般方法是应用全等三角形或等腰三角形的判定和性质,观察本题中要证明的两条线段,它们不在同一个三角形中,且它们分别所在的两个三角形也不全等.因此,要证AB=CD,必须添加适当的辅助线,构造全等三角形或等腰三角形.
现给出如下三种添加辅助线的方法,请任意选择其中一种,对原题进行证明.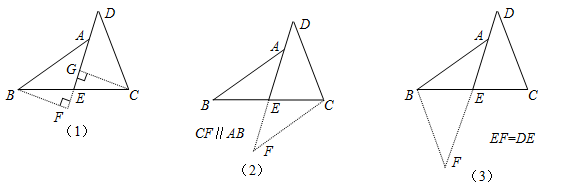
用白铁皮做罐头盒,每张铁片可制盒身16个或制盒底43个,一个盒身与两个盒底配成一套罐头盒,现有150张白铁皮,用多少张制盒身,多少张制盒底,可以正好制成整套罐头盒?
如图,∠AOB=∠COD=90°,OC平分∠AOB,∠BOD=3∠DOE.试求∠COE的度数.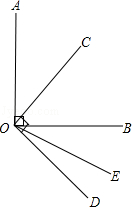
定义新运算:对于任意有理数a,b,都有a※b=a(a﹣b)+1,等式右边是通常的加法,减法及乘法运算,比如:2※5=2×(2﹣5)+1=2×(﹣3)+1=﹣6+1=﹣5.
(1)求(﹣2)※3的值;
(2)若3※x=5※(x﹣1),求x的值.
化简求值:3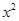 y﹣[2
y﹣[2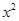 y﹣3(2xy﹣
y﹣3(2xy﹣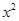 y)﹣xy],其中x=﹣1,y=﹣2.
y)﹣xy],其中x=﹣1,y=﹣2.
一只小虫从某点P出发,在一条直线上来回爬行,假定把向右爬行的路程记为正数,向左爬行的路程记为负数,则爬行各段路程(单位:厘米)依次为:+5,﹣3,+10,﹣8,﹣6,+12,﹣10.
(1)通过计算说明小虫是否回到起点P.
(2)如果小虫爬行的速度为0.5厘米/秒,那么小虫共爬行了多长时间.