某市为增强市民的环境保护意识,面向全市征召义务宣传志愿者.把符合条件的1000名志愿者按年龄分组:第1组[20,25)、第2组[25,30)、第3组[30,35)、第4组[35,40)、第5组[40,45],得到的频率分布直方图如图所示:
(1)若从第3、4、5组中用分层抽样的方法抽取12名志愿者参加广场的宣传活动,应从第3、4、5组各抽取多少名志愿者?
(2)在(1)的条件下,该市决定在这12名志愿者中随机抽取3名志愿者介绍宣传经验,求第4组至少有一名志愿者被抽中的概率;
(3)在(2)的条件下,若ξ表示抽出的3名志愿者中第3组的人数,求ξ的分布列和数学期望.
(本小题满分12分)
如图,台风中心从A地以每小时20千米的速度向东北方向(北偏东 )移动,离台风中心不超过300千米的地区为危险区域.城市B在A地的正东400千米处.请建立恰当的平面直角坐标系,解决以下问题:
)移动,离台风中心不超过300千米的地区为危险区域.城市B在A地的正东400千米处.请建立恰当的平面直角坐标系,解决以下问题:
(1) 求台风移动路径所在的直线方程;
(2)求城市B处于危险区域的时间是多少小时?
(本小题满分12分)
现有8名奥运会志愿者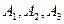 通晓日语,
通晓日语,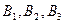 通晓俄语,
通晓俄语, 通晓韩语。从中选出通晓日语、俄语和韩语的志愿者各1名,组成一个小组.
通晓韩语。从中选出通晓日语、俄语和韩语的志愿者各1名,组成一个小组.
(1)求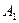 被选中的概率
被选中的概率 ;(2)求
;(2)求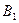 和
和 不全被选中的概率.
不全被选中的概率.
(本小题满分12分)
为了解学生身高情况,某校以10%的比例对全校700名学生按性别进行抽样检查,测得身高情况的统计图如下: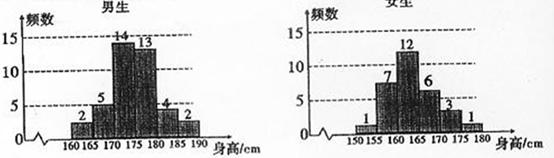
(1)估计该校男生的人数;
(2)估计该校学生身高在170~185cm之间的概率;
(3)从样本中身高在180~190cm之间的男生中任选2人,求至少有1人身高在185~190cm之间的概率.
本小题满分12分)
甲、乙两位学生参加数学竞赛培训.现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次,记录如下:
甲 82 81 79 78 95 88 93 84
乙 92 95 80 75 83 80 90 85
(Ⅰ)用茎叶图表示这两组数据;
(Ⅱ)现要从中选派一人参加数学竞赛,你认为选派哪位学生参加合适?请说明理由.
对于定义域分别为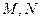 的函数
的函数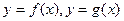 ,规定:
,规定:
函数
(1)若函数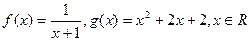 ,求函数
,求函数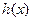 的取值集合;
的取值集合;
(2)若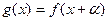 ,其中
,其中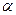 是常数,且
是常数,且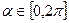 ,请问,是否存在一个定义域为
,请问,是否存在一个定义域为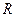 的函数
的函数 及一个
及一个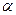 的值,使得
的值,使得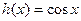 ,若存在请写出一个
,若存在请写出一个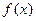 的解析式及一个
的解析式及一个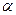 的值,若不存在请说明理由。
的值,若不存在请说明理由。