如图，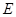
是以
为直径的半圆上异于点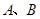
的点，矩形
所在的平面垂直于该半圆所在平面，且
(Ⅰ)求证：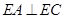
；
(Ⅱ)设平面
与半圆弧的另一个交点为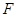
,
①求证：
//;
②若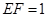
，求三棱锥E-ADF的体积．
画出求a,b中的较大数的程序框图.
下表提供了一种二进制与十六进制之间的转换方法,这也是实际使用的方法之一,利用这个对照表,十六进制与二进制之间就可以实现逐段转换了.求十六进制的C7A16转化为二进制数的算法.
| 二进制 |
000 |
0001 |
0010 |
0011 |
0100 |
0101 |
0110 |
0111 |
| 十六进制 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
| 二进制 |
1000 |
1001 |
1010 |
1011 |
1100 |
1101 |
1110 |
1111 |
| 十六进制 |
8 |
9 |
A |
B |
C |
D |
E |
F |
下面给出一个问题的算法：
S1输入x.
S2若x≤2，则执行S3;否则执行S4.
S3输出-2x-1.
S4输出x2-6x+3.
问题：
(1)这个算法解决的是什么问题？
(2)当输入的x值为多大时，输出的数值最小？
若要按从大到小给7，5，9，3，10五个数排序，试写出算法.
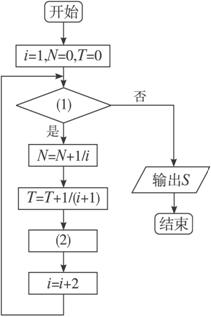
下图所给出的是计算S=1-
+
-
+…+
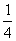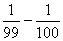的程序框图，请将框图内所缺的式子填充，并写出程序. 