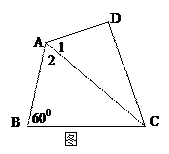设函数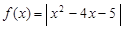 .
.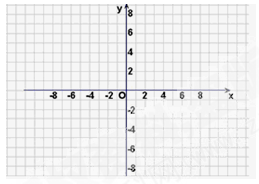
(1)在区间 上画出函数
上画出函数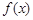 的图象 ;
的图象 ;
(2)设集合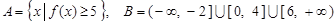 . 试判断集合
. 试判断集合 和
和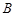 之间的关系,并给出证明.
之间的关系,并给出证明.
(本小题满分10分)
四棱锥P-ABCD中,底面ABCD是正方形,
边长为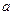 ,PD=
,PD=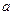 ,PD⊥平面ABCD
,PD⊥平面ABCD
(1)求证: AC⊥PB ;
(2)求二面角A-PB-D的大小;
(3)求四棱锥外接球的半径.
(4)在这个四棱锥中放入一个球,求球的最大半径;
(本小题共10分)
已知数列 满足:
满足: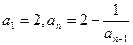 ,
, ,
,
(1)求证:数列 为等差数列; (2) 求数列
为等差数列; (2) 求数列 的通项公式;
的通项公式;
(3)令 ,求证:
,求证: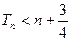 .
.
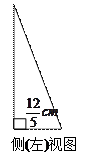
一几何体的三视图如下:
(1)画出它的直观图,并求其体积;
(2)该几何体的哪些面互相垂直?试一一列举出来。

(本小题8分)如图,在正方体ABCD—A1B1C1D1中,已知M为棱AB的中点.
求证:(Ⅰ)AC1//平面B1MC;(Ⅱ)平面D1B1C⊥平面B1MC.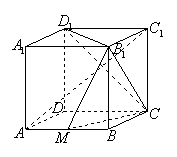
(本小题8分)
如图,在四边形ABCD中,AC平分∠DAB,∠ABC=600,AC=7,AD=6,S△ADC= ,
,
求AB的长.