将矩形ABCD纸片沿对角线AC剪开,得到△ABC和△A′C′D,如图1所示,将△A′C′D的顶点A′与点A重合,并绕点A按逆时针方向旋转,使点D、A(A′)、B在同一条直线上,如图2所示,观察图2可知:与BC相等的线段是______,∠CAC′=______°。
问题探究:如图3,△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB、AC为直角边,向△ABC外作等腰Rt△ABE和等腰Rt△ACF,过点E、F作射线GA的垂线,垂足分别为P、Q,试探究EP与FQ之间的数量关系,并证明你的结论.,
拓展延伸:如图4,△ABC中,AG⊥BC于点G,分别以AB、AC为一边向△ABC外作矩形ABME和矩形ACNF,射线GA交EF于点H,若AB=kAE,AC=kAF,试探究HE与HF之间的数量关系,并说明理由。
如图,在平面直角坐标系中,直线 与双曲线 交于 、 两点, 交 轴于点 ,且 .
(1)求双曲线的解析式;
(2)求点 的坐标,并直接写出 时 的取值范围.

某茶农要对1号、2号、3号、4号四个品种共500株茶树幼苗进行成活实验,从中选出成活率高的品种进行推广,通过实验得知,3号茶树幼苗成活率为 ,把实验数据绘制成图1和图2所示的两幅不完整的统计图.

(1)实验所用的2号茶树幼苗的数量是 株;
(2)求出3号茶树幼苗的成活数,并补全统计图2;
(3)该茶农要从这四种茶树中选择两个品种进行推广,请用列表或画树状图的方法求出1号品种被选中的概率.
在平面直角坐标系 中,已知抛物线的顶点坐标为 ,且经过点 ,如图,直线 与抛物线交于 、 两点,直线 为 .
(1)求抛物线的解析式;
(2)在 上是否存在一点 ,使 取得最小值?若存在,求出点 的坐标;若不存在,请说明理由.
(3)知 , 为平面内一定点, 为抛物线上一动点,且点 到直线 的距离与点 到点 的距离总是相等,求定点 的坐标.

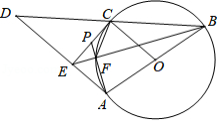
如图, 为圆 的直径, 为圆 上一点, 为 延长线一点,且 , 于点 .
(1)求证:直线 为圆 的切线;
(2)设 与圆 交于点 , 的延长线与 交于点 ,已知 , , ,求 的值.
如图,已知反比例函数 的图象经过点 ,一次函数 的图象经过反比例函数图象上的点 .
(1)求反比例函数与一次函数的表达式;
(2)一次函数的图象分别与 轴、 轴交于 、 两点,与反比例函数图象的另一个交点为 点,连接 、 ,求 的面积.
