已知直线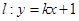 过定点
过定点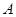 ,动点
,动点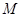 满足
满足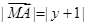 ,动点
,动点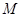 的轨迹为
的轨迹为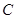 .
.
(Ⅰ)求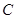 的方程;
的方程;
(Ⅱ)直线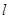 与
与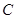 交于
交于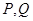 两点,以
两点,以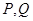 为切点分别作
为切点分别作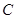 的切线,两切线交于点
的切线,两切线交于点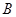 .
.
①求证: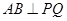 ;②若直线
;②若直线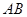 与
与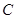 交于
交于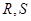 两点,求四边形
两点,求四边形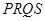 面积的最大值.
面积的最大值.
在数列 中,
中,
(Ⅰ)求数列 的前
的前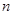 项和
项和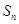 ;
;
(Ⅱ)若存在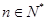 ,使得
,使得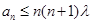 成立,求实数
成立,求实数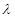 的最小值.
的最小值.
如图1,⊙O的直径AB=4,点C、D为⊙O上两点,且∠CAB=45o,F为 的中点.沿直径AB折起,使两个半圆所在平面互相垂直(如图2).
的中点.沿直径AB折起,使两个半圆所在平面互相垂直(如图2).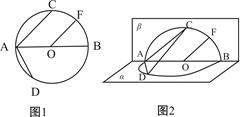
(Ⅰ)求证:OF//平面ACD;
(Ⅱ)在 上是否存在点
上是否存在点 ,使得平面
,使得平面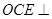 平面ACD?若存在,试指出点
平面ACD?若存在,试指出点 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
已知点 是函数
是函数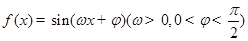 图象上的任意两点,若
图象上的任意两点,若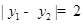 时,
时,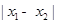 的最小值为
的最小值为 ,且函数
,且函数 的图像经过点
的图像经过点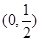 .
.
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)在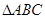 中,角
中,角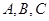 的对边分别为
的对边分别为 ,且
,且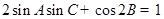 ,求
,求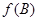 的取值范围.
的取值范围.
某学校为了增强学生对消防安全知识的了解,举行了一次消防安全知识竞赛.其中一道题是连线题,要求将3种不同的消防工具与它们的用途一对一连线,规定:每连对一条得2分,连错一条扣1分,参赛者必须把消防工具与用途一对一全部连起来.
(Ⅰ)设三种消防工具分别为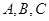 ,其用途分别为
,其用途分别为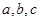 ,若把
,若把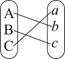 连线方式表示为
连线方式表示为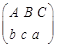 ,规定第一行
,规定第一行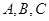 的顺序固定不变,请列出所有连线的情况;
的顺序固定不变,请列出所有连线的情况;
(Ⅱ)求某参赛者得分为0分的概率.