已知抛物线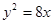 与椭圆
与椭圆 有公共焦点
有公共焦点 ,且椭圆过点
,且椭圆过点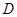
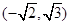 .
.
(1)求椭圆方程;
(2)点 、
、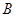 是椭圆的上下顶点,点
是椭圆的上下顶点,点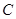 为右顶点,记过点
为右顶点,记过点 、
、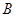 、
、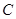 的圆为⊙
的圆为⊙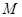 ,过点
,过点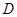 作⊙
作⊙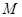 的切线
的切线 ,求直线
,求直线 的方程;
的方程;
(3)过椭圆的上顶点作互相垂直的两条直线分别交椭圆于另外一点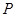 、
、 ,试问直线
,试问直线 是否经过定点,若是,求出定点坐标;若不是,说明理由.
是否经过定点,若是,求出定点坐标;若不是,说明理由.
已知方向向量为 的直线
的直线 过点
过点 和椭圆C:
和椭圆C: 
 的焦点
的焦点 ,且椭圆C的中心关于直线
,且椭圆C的中心关于直线 的对称点在椭圆的右准线上, 直线
的对称点在椭圆的右准线上, 直线 过点
过点 交椭圆C于M、N两点.
交椭圆C于M、N两点.
(1)求椭圆C的方程;
(2)若设 是椭圆C的右焦点,若
是椭圆C的右焦点,若 ,求直线
,求直线 的方程;
的方程;
(3)设 (
( 为坐标原点),当直线
为坐标原点),当直线 绕点
绕点 转动时,求
转动时,求 的取值范围.
的取值范围.
已知圆C满足:①截Y轴所得弦长为2,②被X轴分成两段弧,其弧长的比为3∶1,③圆心到直线 :
: 的距离为
的距离为 .
.
(1)求圆C的方程;
(2)过点 的直线能否与圆C相切,若相切,求切线方程,若不相切,说明理由.
的直线能否与圆C相切,若相切,求切线方程,若不相切,说明理由.
已知椭圆C: ,直线
,直线 过点P
过点P 交椭圆C于A、B两点.
交椭圆C于A、B两点.
(1)若P是AB中点,求直线 的方程及弦AB的长;
的方程及弦AB的长;
(2)求弦AB中点M的轨迹方程.
已知函数 ,
, .
.
(1)求函数 的最小正周期和单调增区间;
的最小正周期和单调增区间;
(2)说明 的图象可以由函数
的图象可以由函数
 的图象经过怎样的变换得到.
的图象经过怎样的变换得到.
设函数 ,若
,若 且
且 .
.
求证: .
.