(1)观察与发现:将矩形纸片AOCB折叠,使点C与点A重合,点B落在点B′处(如图),折痕为EF.小明发现△AEF为等腰三角形,你同意吗?请说明理由.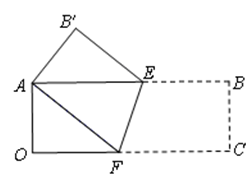
(2)实践与应用:以点O为坐标原点,分别以矩形的边OC、OA为x轴、y轴建立如图所示的直角坐标系,若顶点B的坐标为(9,3),请求出折痕EF的长及EF所在直线的函数关系式.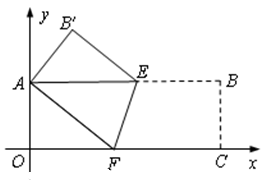
(本题8分)如图,数轴上有三个点A、B、C,表示的数分别是-4、-2、3,请回答: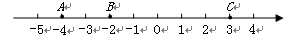
(1)若将点B向左移动5个单位后,三个点所表示的数中,最小的数是;
(2)若使C、B两点的距离与A、B两点的距离相等,则需将点C向左移动
个单位;(3)若移动A、B、C三点中的两个点,使三个点表示的数相同,移动方法有种,其中移动所走的距离和最大的是个单位;
(4)若在原点处有一只小青蛙,一步跳1个单位长. 小青蛙第1次先向左跳1步,第2次再向右跳3步,然后第3次再向左跳5步,第4次再向右跳7步,…,按此规律继续跳下去,那么跳第100次时,应跳步,落脚点表示的数是;跳了第n次(n是正整数)时,落脚点表示的数是.
(5)数轴上有个动点表示的数是x,求|x-2︱+|x+3|的最小值.
(本题8分)小王上周末买进股票1000股,每股20元。下表为本周内每天该股票下午收盘时的涨跌情况(正数表示相对前一个交易日上涨的价格,负数表示相对前一个交易日下跌的价格)
| 星期 |
一 |
二 |
三 |
四 |
五 |
| 每股涨跌(元) |
+4 |
+3.5 |
-1.5 |
-2.5 |
-6 |
⑴星期四收盘时,每股多少元?
⑵本周内哪一天股票下午收盘时价格最高?最高是多少元?
⑶已知买进股票需付0.15%的手续费,卖出时需付成交金额0.1%的交易税和0.15%的手续费,如果小王本周星期五收盘前将股票全部卖出,他的收益情况如何?请写出具体过程。
(本题6分)小黄做一道题“已知两个多项式A,B,计算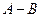 ”.小黄误将
”.小黄误将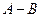 看作
看作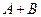 ,求得结果是
,求得结果是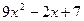 .若
.若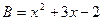 ,请你帮助小黄求出
,请你帮助小黄求出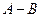 的正确答案.
的正确答案.
(本题8分)2009年十月一日凌晨2点,参加我国建国60周年阅兵活动的各个部队方阵已经在东长安街集结完毕。阅兵副总指挥为了协调各项准备工作,他的指挥车在东西走向的东长安大街来回奔波于各个方阵之间,如果规定向东为正,向西为负,到早上7点整他的行车里程(单位:千米)如下:+14,-2,+5,-1,+10,-3,-2,+12,+4,-9,+8(1)到早上7点整时,他的指挥车距出发点多远?
(2)若指挥车汽车耗油量为8升/100千米,这天下午指挥车共耗油多少升?
(本题8分)已知一个三位数的百位数字比十位数字大1,个位数字比十位数字小1,设十位数字为n。(1)用关于n的式子表示这个三位数(2)这个三位数一定能被3整除吗?说明理由。